\(\def\vector#1{\boldsymbol{#1}}\)

格子暗号

2020年4月1日 #NTRU

概要

格子暗号 (lattice-based cryptography) は多次元の格子構造を用いた公開鍵暗号スキーム。証明可能な強力なセキュリティの保証や量子計算耐性、完全準同型暗号へ応用可能といった特性を持っている。

\(n\) 次元の格子 \(\mathcal{L}\) は \(n\) 次元の実ベクトル空間 \(\mathbb{R}^n\) の離散加法部分群である。格子は \(\mathbb{R}^n\) 上の線形独立ベクトル \(b_1,\ldots,b_m\) の整数係数の組合せによって生成され、この \(m\) 個のベクトルは格子の基底である。

概要
格子問題
NTRU 暗号
参考文献

格子問題

格子暗号は格子問題が困難であるという仮定の下に成り立っている。

最短ベクトル問題

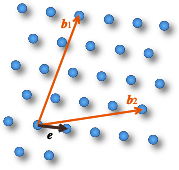
最短ベクトル問題 (SVP; short vector problem) はある格子 \(\mathcal{L}\) の基底が与えられたとき、\(\mathcal{L}\) 上の格子点を結ぶベクトルで長さが最小となる非ゼロベクトルを見つける問題。

Fig 1 の例では (図中 \(\vector{e}\) は \(\vector{\sigma}\) の間違い)、あるベクトル \(\vector{b}=\{\vector{b}_1,\vector{b}_2\}\) を基底とする格子 \(\mathcal{L}\) (つまり \(\mathcal{L}\) を構成する全ての格子点が \(\vector{b}\) の整数係数一次結合で表すことができる) において、格子の点を結ぶベクトルで最も小さいノルムを持つ \(\vector{\sigma}\) を得る問題である。

\(s_1\), \(s_2\) を任意の整数としたとき、式 (\(\ref{svp}\)) を満たす最も小さい \(\vector{\sigma}\) を見つけることは困難である (効率的に見つける方法は見つかっていない)。\[ \begin{equation} s_1 \vector{b}_1 + s_2 \vector{b}_2 = \vector{\sigma} \label{svp} \end{equation} \]

最近接ベクトル問題

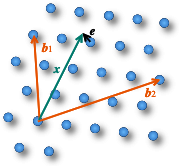
最近接ベクトル問題 (CVP; closest vector problem) は格子の基底と対象のベクトルが与えられたときに、対象に最も近い格子点を求める問題。

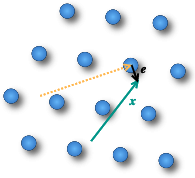
Fig 2 の例では、あるベクトル \(\vector{b}=\{\vector{b}_1,\vector{b}_2\}\) を基底とする格子 \(\mathcal{L}\) において、ある対象ベクトル \(\vector{x}\) と最も近い格子の点とのベクトル差 \(\vector{e}\) を得る問題である。

\(\vector{s}= (s_1,s_2,\ldots)\) を任意の整数のベクトルとしたとき、\(\vector{b}\) と \(\vector{x}\) から式 (\(\ref{cvp}\)) を満たす \(\vector{s}\) や (最小のノルムを持つ) \(\vector{e}\) を見つけることは困難である。\[ \begin{equation} \left( \begin{array}{cccc} \vector{b}_1 & \vector{b}_2 & \cdots & \vector{b}_n \end{array} \right) \left( \begin{array}{c} s_1 \\ s_2 \\ \vdots \\s_n \end{array} \right) + \vector{e} = \vector{x} \label{cvp} \end{equation} \]

LWE 問題

LWE 問題 (learning with error problem) は誤差 (ノイズ) を付与した多元連立一次方程式を解く問題。最近接ベクトル問題における基底ベクトルの整数係数一次結合の概念を行列式に拡張したものとも言える。式 (\(\ref{lwe}\)) において行列 \(\vector{A}\) と \(\vector{x}\) が与えられたとき \(\vector{s}\) を求める問題である。\[ \begin{equation} \vector{A} \vector{s} + \vector{e} \equiv \vector{x} \pmod{q} \label{lwe} \end{equation} \] 行列式で記述すると以下のようになる。\[ \left( \begin{array}{cccc} a_{1,1} & a_{1,2} & \cdots & a_{1,m} \\ a_{2,1} & a_{2,2} & \cdots & a_{2,m} \\ \vdots & \vdots & & \vdots \\ a_{n,1} & a_{n,2} & \cdots & a_{n,m} \\ \end{array} \right) \left( \begin{array}{c} s_1 \\ s_2 \\ \vdots \\s_m \end{array} \right) + \left( \begin{array}{c} e_1 \\ e_2 \\ \vdots \\e_n \end{array} \right) \equiv \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\x_n \end{array} \right) \pmod{q} \]

NTRU 暗号

NTRU 暗号は 2005 年に Oded Regev によって定義された格子暗号。格子の基底ベクトルの一次線形結合から最も近い格子点を見つけ出す最近接ベクトル問題の困難性を前提としている。ここでは単純化して 2 次元空間での NTRU 暗号の構造を説明する。

設定

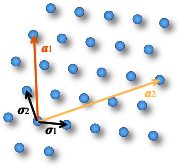
2 次元空間上の直行しない 2 つのベクトル \(\vector{\sigma}=(\vector{\sigma}_1,\vector{\sigma}_2)\) を基底とする格子 \(\mathcal{L}_\vector{\sigma}\) を仮定し、\(\vector{\sigma}\) の整数係数線形結合によって表される \(\mathcal{L}_\vector{\sigma}\) 上の 2 つのベクトル \(\vector{A}=(\vector{a}_1,\vector{a}_2)\) を定義する (Fig 3)。

ここで \(\vector{\sigma}\) が秘密鍵、\(\vector{A}\) が公開鍵に相当する。最短ベクトル問題により \(\vector{A}\) から \(\vector{\sigma}\) を求めることは困難であることに注意。

Fig 3. 格子の基底 \(\vector{e}\) と \(\vector{A}\)。

暗号化

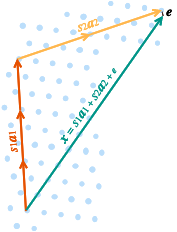
まず暗号者は平文を小さなベクトル \(\vector{e}\) にエンコードする。次に任意の整数 \(s_1\), \(s_2\) を決定し、\(\vector{A}\) の整数係数一次線形結合のベクトルを \(\vector{x}_0 = s_1 \vector{a}_1 + s_2 \vector{a}_2\) とする。\(\vector{x}_0\) に \(\vector{e}\) を加えたベクトル \(\vector{x}=\vector{x}_0 + \vector{e}\) を暗号文とする。

ここで、ノイズ (誤差) \(\vector{e}\) を加えた \(\vector{x}=\vector{x}_0+\vector{e}\) から最も近い格子点 \(\vector{x}_0\) を求めることは最近接ベクトル問題により困難という点が重要である。すなはち、第三者は \(\vector{A}\) と \(\vector{x}\) が分かったとしても、それらから \(\vector{x}_0\) や \(\vector{e}\) を求めることは困難である。

NTRU 暗号では \(\vector{x}\) に最も近い格子点が \(\vector{x}_0\) でなければならないことに注意。\(\vector{\sigma}\) を決定するために格子点がある程度以上の距離でなければならない。\(\vector{e}\) はしばしば正規分布に従う乱数を使用する。

復号化

復号者は基底 \(\vector{\sigma}\) を使用して暗号文 \(\vector{x}\) から最も近い格子点 \(\vector{x}_0\) を特定し、その差異、つまり平文 \(\vector{e}\) を算出することができる。

以上より、この例でのセキュリティは以下の仮定に基づいていることがわかる。

格子の基底 \(\vector{\sigma}\) を知っている者は \(\vector{x}\) に最も近い格子点を容易に計算することができる。
基底 \(\vector{\sigma}\) を知らない者が \(\vector{a}_1\), \(\vector{a}_2\) を用いて基底 \(\vector{e}\) を効率的に算出する方法が分かっていない (公開鍵から秘密鍵を推測できない)。これは最短ベクトル問題が困難であるという仮定である。
基底 \(\vector{\sigma}\) を知らない者が \(\vector{a}_1\), \(\vector{a}_2\) を用いて \(\vector{x}\) との距離が最も小さくなるような格子点 \(\vector{x}_0\) を算出する \(s_1,s_2\) の組合せを効率的に計算・推定する方法は今のところ分かっていない (つまり公開鍵と暗号文から平文を推測できない)。

この概念はより一般的な \(n\) 次元空間上の \(m\) 個のベクトルへ拡張することができる。式 (\(\ref{cvp}\)) において \(\vector{b}\) 及び \(\vector{x}\) が分かったとしても \(\vector{s}\) や \(\vector{e}\) を求めることが困難であるという仮定を表している。