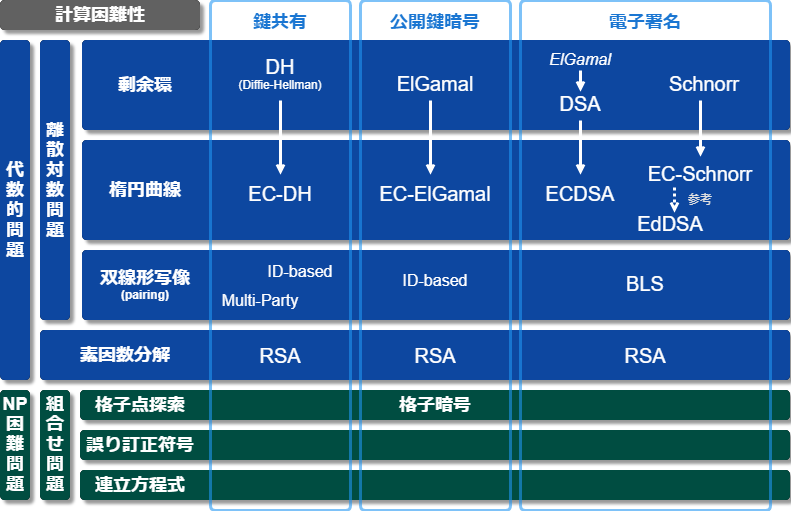
公開鍵暗号アルゴリズム

概要

公開鍵は「A から B を計算するのは容易だが B から A を計算するのは困難」といった計算の非対称性を利用した暗号アルゴリズム。公開鍵アルゴリズムを応用した技術として鍵共有、暗号、電子署名が広く使われている。また近年では公開鍵の特性を利用してゼロ知識証明といったようなアルゴリズムの研究も進んでいる。

目次

離散対数問題と公開鍵暗号

離散対数問題に基づく暗号アルゴリズムは古くから研究されてきたが、公開鍵暗号が世間に広く利用されるようになったのは素因数分解に基づく RSA を待たなければならなかった。しかし旧来の欠点を克服した DSA や、楕円曲線への応用によって、近年では RSA に比べてより高いパフォーマンスを得られるようになった。…

2019年12月15日(Sun) #DLP #DH #ElGamal #DSA #Schnorr

楕円曲線暗号

楕円曲線は離散対数問題に対して有限体よりも効率的で高いセキュリティを持つ有限体である。これらはどちらも DLP の数式上の循環群 \(G\) として使用できるため、旧来の Diffie-Hellman や ElGamal といったアルゴリズムをほぼそのまま楕円曲線に置き換えることができる。…

2019年12月15日(Sun) #ECDH #ECC #ECDSA #EdDSA #ed25519 #ed448

RSA 暗号

RSA 公開鍵暗号 (RSA public-key encryption) は大きな数の素因数分解の困難性を利用した公開鍵暗号。最初の実用的な公開鍵暗号で 2000 年に特許が切れている。より鍵の小さい楕円曲線暗号に置き換えられつつあるが現在においても広く利用されている。…

2019年12月15日(Sun) #RSA

ペアリング暗号

ペアリング暗号 (pairing-based cryptography) は双線形写像 (bilinear map) の構造を持った暗号アルゴリズム。楕円曲線暗号ではある同一の群 \(G\) 上での写像 \(e:G \times G \to G\) の写像だったが、ペアリングでは 2 つの暗号化群から別の群への写像 \(e:G_1 \times G_2 \to G_T\) という構造を持つ。…

2019年9月16日(Mon) #Pairing #IBE #BLS

属性ベース暗号

属性ベース暗号 (ABE; attribute-based encryption) は特定の属性を持った対象者のみが情報を復号化できる暗号方式。共通鍵暗号や公開鍵暗号は暗号化/復号化に使用する鍵が 1:1 であるのに対して、それが 1:n や n:1 という特徴を持つ。…

2019年8月21日(Wed) #ABE 作業中

格子暗号

格子暗号 (lattice-based cryptography) は多次元の格子構造を用いた公開鍵暗号スキーム。証明可能な強力なセキュリティの保証や量子計算耐性、完全準同型暗号へ応用可能といった特性を持っている。…

2020年4月1日(Wed) #NTRU