公開鍵暗号アルゴリズム
RSA暗号 ::

楕円曲線暗号

Takami Torao #ECDH #ECC #ECDSA #EdDSA #ed25519 #ed448
  • このエントリーをはてなブックマークに追加

概要

楕円曲線は離散対数問題に対して有限体よりも効率的で高いセキュリティを持つ有限体である。これらはどちらも DLP の数式上の循環群 \(G\) として使用できるため、旧来の Diffie-Hellman や ElGamal といったアルゴリズムをほぼそのまま楕円曲線に置き換えることができる。楕円曲線への置き換えによりいくつかの欠点が克服できる他、より小さな鍵サイズと計算量で同程度のセキュリティを確保することができるようになった。

Table of Contents

  1. 概要
  2. 楕円曲線離散対数問題
  3. 楕円曲線 Diffie-Hellman 鍵共有
  4. 楕円曲線暗号
  5. 楕円曲線 DSA (ECDSA)
  6. エドワーズ曲線 DSA (EdDSA)
  7. 参考文献

楕円曲線離散対数問題

楕円曲線暗号アルゴリズムは有限体上の乗法群の離散対数問題の困難性を楕円曲線上の加法群で構成したもの。ECDLP は DLP や素因数分解より困難であると考えられていることから、実用上優れていると考えられている。

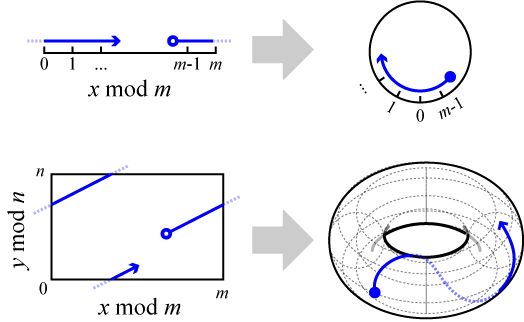
有限体を 2 次元のユークリッド座標系に拡張するとドーナツ状の構造 (トーラス) となる。トーラスは楕円関数の像である楕円曲線を複素面に拡張した形と同じであることから、この拡張によって離散対数問題の有限体に楕円曲線を利用できることが分かる。

2 次元ベクトル空間においてベクトル \(P\) が明らかなとき、任意の整数 \(x \in \mathbb{Z}\) に対する \(P^x\) の点を求めることは容易だが、点 \(P^x\) から \(x\) を求めることは難しい。このような \(P\) と \(P^x\) が与えられたときに \(x\) を求める問題を楕円離散対数問題 (ECDLP, elliptic curve DLP) と呼ぶ。

楕円曲線 Diffie-Hellman 鍵共有

楕円曲線 Diffie-Hellman 鍵共有 (ECDH 鍵共有) は Diffie-Hellman 鍵共有における有限体を楕円曲線に応用した鍵共有アルゴリズム。パラメータとして、ある位数 \(n\) の楕円曲線 \(E\) とその楕円曲線上のベースポイント \(G\) が共有されていると仮定する。

  1. A は秘密鍵 \(S_a \in \{1, \ldots,n-1\}\) をランダムに選択して公開鍵 \(S_a G\) を公開する。
  2. B は秘密鍵 \(S_b \in \{1, \ldots, n-1\}\) をランダムに選択して公開鍵 \(S_b G\) を公開する。
  3. A と B の双方が相手の公開鍵に自分の秘密鍵を乗算することで共通の値 \(S_a S_b G\) を共有することができる。

A も B も送受信する情報は公開鍵 \(S_x G\) のみであり、楕円曲線上の離散対数問題が解けない限り、秘密鍵 \(S_x\) を復元することはできない。

楕円曲線 DH 鍵共有は DH 鍵共有より計算速度が速く鍵長も小さい。このためセッションごとに秘密鍵を作り直し共有するコストが低く、暗号通信に前方秘匿性 (PFS; perfect forward security, 秘密鍵が漏洩しても過去に遡って復号化できない性質) を持たせやすくなる。

楕円曲線暗号

楕円曲線暗号 (ECC) は ElGamal 暗号における有限体を楕円曲線に応用した公開鍵暗号アルゴリズム。位数 \(n\) の楕円曲線 \(E\) とその楕円曲線上のベースポイント \(G\) が共有されていると仮定する。

  • 鍵生成: A は秘密鍵 \(S_a \in \{1,\ldots,n-1\}\) をランダムに選択し公開鍵 \(P_a = S_a G\) を公開する。
  • 暗号化: \(E\) 上の点として表現されている平文を \(m\) とする。B は整数 \(r\) をランダムに選択し、暗号文 \((rG, m+rP_a)\) を A に送信する。
  • 復号化: A は暗号文と秘密鍵 \(S_a\) を使用して \((m + rP_a) - S_a r G = m + rS_aG - rS_aG = m\) により平文を復元することができる。

ElGamal 暗号と同様に、暗号時に乱数 \(r\) を使用するため秘密鍵 \(a\) や平文 \(m\) が同じであっても暗号文は毎回異なる値となる。

楕円曲線暗号は RSA 暗号と比較してより小さな鍵で同等の安全性を持つ特徴がある。以下は [3] より引用。

RSA 暗号 1024 1219 2048 2832 11393
楕円曲線暗号 138 152 206 245 497

楕円曲線 DSA (ECDSA)

一般に ECDSA と呼ばれる楕円曲線 DSA は DSA における有限体を楕円曲線に応用した電子署名アルゴリズム。任意のデータ列を \(E\) 上の点に変換するハッシュ関数 \(h\) と \(q = \min \{ n | nP=0, n \gt 0\}\) が共有されていると仮定する。

  • 鍵生成: A は秘密鍵 \(S_a \in \{1, \ldots,n-1\}\) をランダムに選択し公開鍵 \(S_a G\) を公開する。
  • 署名: A は整数 \(r\) をランダムに選択する。\(rG\) の \(x\) 座標を \(x\) とする。平文 \(m\) に対して \(s = \frac{h(m) + xS_a}{r} \bmod q\) とし \((x,s)\) を署名とする。
  • 検証: 公開鍵 \(S_a G\) と与えられた平文 \(m\)、署名 \((x,s)\) に対して \[ \frac{h(m)}{s} G + \frac{x}{s} P_a = \frac{h(m) + xS_a}{s} G = rG \] を計算する。署名時の設定より、得られた \(rG\) の \(x\) 座標が \(x\) と等しければ署名は有効である。

エドワーズ曲線 DSA (EdDSA)

EdDSA は楕円曲線の一種で Edwards 曲線を使用した署名アルゴリズム。Curve25519 曲線を使用した Ed25519 と、Ed25519 と比べて処理は遅いがより暗号強度の強い Ed448 がある。

DSA や ECDSA は署名/検証ステップで除算のコストが必要だったが、Ed25519 は除算を必要としない Schnorr 署名を応用している。他にも現代的な CPU 設計を強く意識した実用的な設計が成されていて高速な署名アルゴリズムである。実装コードも小さく、本の論文では L1 キャッシュに乗るサイズである。その他にも実践的な多くの特徴を持つ (論文参照)。

署名のための秘密鍵とは別に、秘密鍵を生成するためのシークレットと呼ばれる整数が存在する。

  • 設定: Curve25519 は \(p=2^{255}-19\) の群。
  • 鍵生成: シークレット \(x\) をランダムに選択する。

Ed448 は Curve25519 とは別の曲線を使用しており、処理は遅いが Ed25519 より暗号強度が高い。

参考文献

  1. 辻井重男, 笠原正雄, 有田正剛, 境隆一, 只木孝太郎, 趙晋輝, 松尾和人, "暗号理論と楕円曲線", 森北出版 (2008)
  2. J.A. ブーフマン, "暗号理論入門 原書第3版, 丸善出版 (2012)
  3. 光成滋生, "クラウドを支えるこれからの暗号技術", 秀和システム (2015)
  4. Daniel J. Bernstein1, Niels Duif, Tanja Lange, Peter Schwabe, and Bo-Yin Yang (2011) "High-speed high-security signatures"