離散対数問題と公開鍵暗号
 概要
概要
離散対数問題に基づく暗号アルゴリズムは古くから研究されてきたが、公開鍵暗号が世間に広く利用されるようになったのは素因数分解に基づく RSA を待たなければならなかった。しかし旧来の欠点を克服した DSA や、楕円曲線への応用によって、近年では RSA に比べてより高いパフォーマンスを得られるようになった。このページでは離散対数問題と、剰余環に基づく公開鍵暗号アルゴリズムについて解説する。
Table of Contents
 計算困難問題
計算困難問題
計算複雑性の文脈ではたかだか多項式時間 (polynomial time) で解くことのできるアルゴリズムは効率的であり、そのようなアルゴリズムは暗号理論において安全ではないと認識されている。
アルゴリズムの具体的な計算量はビット単位を手作業で計算したステップ数で数えることができる。例えば \(a\) と \(b\) を 2 進数で展開される自然数とし、それぞれのビット長を \(m_a\), \(m_b\) とする。1 ビット単位の和の計算量を \(O(1)\) としたとき、四則演算はそれぞれ:
- 加法: \(O(\max(m_a, m_b))\)
- 乗法: \(O(m_a m_b)\)
- 除法: \(a \div b\) で商 \(q\) と剰余を求めるとき \(O(m_b q)\)
の時間で表すことができる。
パラメータとして整数 \(z_1, \ldots, z_n\) を入力したときの実行時間が \(O(m_{z_1}^{e_1}m_{z_2}^{e_2} \ldots m_{z_n}^{e_n})\) の形式で表されるのであれば、そのアルゴリズムは多項式時間アルゴリズムである。ここで \(e_i\) は負でない整数を表している。特に、\(O\) の係数と指数 \(e_i\) が小さい場合は現実的なコンピュータの計算能力で効率的に解が得られるアルゴリズムである。
現代の暗号で広く実用されている公開鍵暗号技術は指数時間アルゴリズムの特性を持つ (と考えられている) 離散対数問題と素因数分解に基づいている。これら以外にも歴史的に暗号システムの基礎としての計算困難問題がいくつか提案されている [HoECC05]。
- ナップザック問題 (部分集合合計問題): 要素の合計がある整数 \(s\) と等しくなるように、ある整数集合の部分集合を決定する。最初に提案された低密度の問題は多項式時間で破られている。まだ破られていない問題もいくつか存在するが、今のところそれほど適用されてはいない。
- NTRU 暗号および署名: ある有限体 \(\mathbb{F}_q\) の多項式環で \(X^N-1\) を法とするスパース多項式の回復問題に基づいたシステムで、格子に転用して最短ベクトル問題に変換することができる。処理は非常に高速であるためセキュリティを確保するパラメータの選択に関心が持たれている。
- 多変量二次方程式 (MQ): 一般的な MQ 問題は NP 完全だが、暗号システムを構築するために提案された多くはそうではない。隠しフィールド方程式 (HFE; hidden field equations) は計算能力が進歩した今でも安全と考えられており、HFE の証明可能な変種を見つけ出す分野は依然として活発に研究されている。
離散対数問題や素因数分解は強力な量子コンピュータの仮定の下で両者とも既に多項式時間で解くアルゴリズムが存在している。現代のネットワークで DH や ECDSA、RSA といった公開鍵暗号アルゴリズムがもはや安全ではないとなれば世界的に大きな混乱を招くことが予想されるため、NP 困難などの量子計算耐性を持つ計算困難問題に基づく暗号アルゴリズムの研究が進められている。
 離散対数問題
離散対数問題
素数位数 (prime order) \(p\)、生成元 (generator) \(g\) を持つ群を \((G, \ast)\) としたとき、核 (kernel) \(p\mathbb{Z}\) を持つ整数の加法群 \((\mathbb{Z}_{/p\mathbb{Z}},+)\) から \((G,\ast)\) への同型写像を \(\varphi\) とする。\[ \begin{array}{rcl} \varphi: \mathbb{Z} & \to & G \end{array} \] この \(\varphi\) の逆写像に相当する計算問題を (\(g\) に基づく) 離散対数問題 (DLP; discrete logarithm problem) と呼ぶ。例えば \(G\) が乗法群であれば \(y = \varphi(x) = g^x\) となるような整数 \(x \in \mathbb{Z}_{/p\mathbb{Z}}\) を求める問題である。
長らく乗法群 (特に剰余環; 剰余環自体は加法群でも乗法群でもある) を用いて研究されてきた経緯から、この離散対数 \(x=\log_g \varphi(x)\) を求める問題は離散対数問題と呼ばれているが、現在広く利用されている楕円曲線が加法群 \((E,+)\) であるように乗法群のみを対象にしているわけではない。楕円曲線でもこの歴史的経緯から写像 \(\varphi(x)=xP\) の \(x\) は離散対数と呼ばれている。
\(\log_g y\) で表される \(y\) の離散対数は群の位数が素数である場合にのみ一意となる。言い換えると、位数が素数でない乗法群は離散対数が重解を持つ、つまり同型写像 \(\varphi\) が存在しないことになり、離散対数問題の対象としては使用できない。
一般的に離散対数問題に基づく暗号システムでは乗法群として巡回群 (cyclic group) が用いられており、公開鍵や秘密鍵、署名の値は \(G\) 上の元 (element) として表されている。
 乗法群に基づく離散対数問題
乗法群に基づく離散対数問題
\(g^x \bmod p\) で表される式を冪剰余 (modular exponentiation) と呼ぶ。離散対数問題を利用する古典的な暗号では素数 \(p\) の冪剰余が生成する巡回群 \(G=\) \(\{g^x \bmod p \ | \ x \in \mathbb{Z}\}\) \(=\{1,2,\ldots,p-1\}\) を使用する。冪剰余は巨大な \(p\) に対しても計算が容易であり、またその像は \(p\) より小さい値の集合 (有限体) を形成することからデータ幅が決まるためコンピュータで扱うのに都合が良い。
 冪剰余による乗法群
冪剰余による乗法群
被除数 \(a\)、除数 \(m \gt 0\) をそれぞれ整数とし、\(0 \le r \lt m\) の下で \(a = qm + r\) となるような整数 \(q, r\) をそれぞれ商、剰余と呼ぶ。剰余 \(r\) はいわば \(a\) を \(m\) で割った余りであり \(r = a \bmod m\) と表す (\(a\) が負値であっても \(0 \le r \lt m\) の範囲とする点に注意)。また、\(m\) に対する \(a\) と \(b\) の剰余が等しいとき \(a \equiv b \pmod{m}\) と表す。
冪剰余の乗算の剰余は、その被除数に対する乗算の剰余と等しい。\[ \begin{equation} ((a \bmod m) \times (b \bmod m)) \bmod m = (a \times b) \bmod m \label{multi} \end{equation} \] これは冪剰余の集合の中で乗法が定義できることと等価である。また式 (\(\ref{multi}\)) において \(a \bmod m \equiv 1\) のとき右辺は \(b \bmod m\) と等しくなるなることから \(e=1\) を単位元ととする乗法群 \((G, \times)\) を生成する。
正の整数における \(m\) を法とする剰余類 \(\mathbb{Z}_{/m\mathbb{Z}}=\{0,1,\ldots,m-1\}\) が乗法に対して巡回群 \(G\) となる条件について考える。
- \(x \equiv 1 \pmod{m}\) のとき (\(\ref{multi}\)) より \(x \times (a \bmod m) \equiv a \bmod m\) であることから単位元は \(e=1\) と考えることができる。しかし \(0 \times x = 0\) より 0 に対して 1 は単位元となり得ない。従って 0 は除外する必要があり \(G=\{1,2,\ldots,m-1\}\) である。
- 位数 \(m\) がある整数 \(a \lt m\) と \(b \lt m\) の積 \(a\times b=m\) で表されるとき、\(a\) と \(b\) は共に群の要素でありながら \(a \times b \equiv 0 \pmod{m}\) となり群 \(G\) に属さない像となるため乗法が閉じていないことになる。これを回避するために位数 \(m\) を素数とすると都合がよい (\(m\) と素でない要素を除外してもよいがデータサイズに対して要素数が減るので効率が悪い)。
乗法による巡回群は直感的に Fig 1. のような時計盤に似た構成と考えることができる。\(g\) の \(x\) 乗は時計盤上を何周も移動してある位置に定まるが、結果として得られた位置 \(y\) から指数 \(x\) を求める問題は、\(g\), \(p\), \(g^x \bmod p\) が与えられたときに \(x\) を求める離散対数問題に相当する。
一般に以下の条件を満たす乗法群の DLP を現在のコンピュータで解くのは現実的ではないと考えられている。
- \(p\) が 1024 ビット以上の素数であり、\(p-1\) の約数の中に \(p\) に近いサイズの素数 \(q\) が存在する。
- \(i=1,\ldots,q-1\) に対して \(g\) は \(g^i \not\equiv 1 \bmod p\) となる値である。
\((p,q,g)\) の組を DH パラメータや DH 群などと呼ぶ。
 冪剰余の効率的な計算
冪剰余の効率的な計算
乗法群は乗算を繰り返すことでべき乗を計算することができる。ここで \(2^n \bmod m\) について考えると、まず \(n=0\) の時に 1 であり、\(n=m-1\) で再び 1 となり、以後 \(2(m-1), 3(m-1), \ldots\) のたびに 1 となることを繰り返すことが分かる。つまり \(m-1\) ごとに同じ値を繰り返すことから以下の式が成り立つ。\[ 2^n = 2^{q(m-1)+r} = 2^{q(m-1)} \times 2^r \equiv 2^r \pmod{m} \]
例えば \(2^{16}\) は \(2^{2 \times 6 + 4} \equiv 2^4 \pmod{7}\)、つまり \(2^{16} \bmod 7 = 2^4 \bmod 7 = 2\) と計算を簡略化できる。これは \(2^{16}\) を計算して剰余を求めるよりも遙かに容易に答えを導くことができる。一般化すると以下のように表すことができる。\[ \begin{equation} a^n \equiv a^{n \bmod (m-1)} \pmod{m} \label{modexp} \end{equation} \]
このように冪剰余の計算式は指数が巨大な数であっても効率的に計算することができる。実装向けのアルゴリズムではモンゴメリ冪乗 (Montgomery modular multiplication) などがある。
 乗法群の生成元
乗法群の生成元
位数 \(p\) を持つ乗法群 \(G\) の元が \(0 \lt g \lt p\) のべき乗で表されるとき、\(g\) を \(G=\{g^0,g^1,\ldots,g^{p-1}\}\) の生成元 (generator)または原始根、原始元と呼ぶ。
\(G\) を循環群として扱うために \(\{g^0,g^1,\ldots,g^{p-1}\}\equiv\{1,2,\ldots,p-1\} \pmod{p}\) となるケースについて考える (\(g^n\) が必ずしも \(n\) に対応していないことに注意)。
- \(g^0=1\) (単位元 \(e\)) である。
- \(m \ge 1\) かつ \(g^m \bmod p \equiv 1\) を満たす最初の \(m\) 以降の値は繰り返しとなり新しい元は出現しない。したがって \(G = \{1,g,g^2,\ldots,g^{m-1}\}\) と表すことができる。(\(\ref{modexp}\)) より \(g^m \equiv g^{m \bmod (p-1)} \equiv 1 \pmod{p}\) を満たす最小の \(m\) は \(p-1\) である。
\(G\) は \(p\) を法とする剰余の集合であることから、\(G\) の位数が \(|G| = m = p - 1\) であれば、\(G\) は \(1\) から \(p-1\) のすべての整数で構成されていることを意味する。そして \(0 \lt g \lt p\) より \(g \in G\) は明かである。
つまり、ある元 \(g \in G\) が \(G\) の生成元であるためには \(g^{p-1} \bmod p \equiv 1\) であり、\(g^m \bmod p \equiv 1\) となるような \(0 \lt m \lt p-1\) が存在しないことが確認できれば良い。
離散対数問題を扱うときの生成元 \(g\) は \(2,3,\ldots\) といった小さな数値であっても良い。
 Diffie-Hellman 鍵共有
Diffie-Hellman 鍵共有
Diffie-Hellman 鍵共有 (DH key exchange) は乗法群を用いた離散対数問題に基づいて end-to-end で鍵を交換するアルゴリズム。1976 年に提案された。A と B とが安全ではない通信チャネルを用いて秘密の鍵を共有することができる。鍵が大きく計算量も多いが現在でも TLS で使われている。
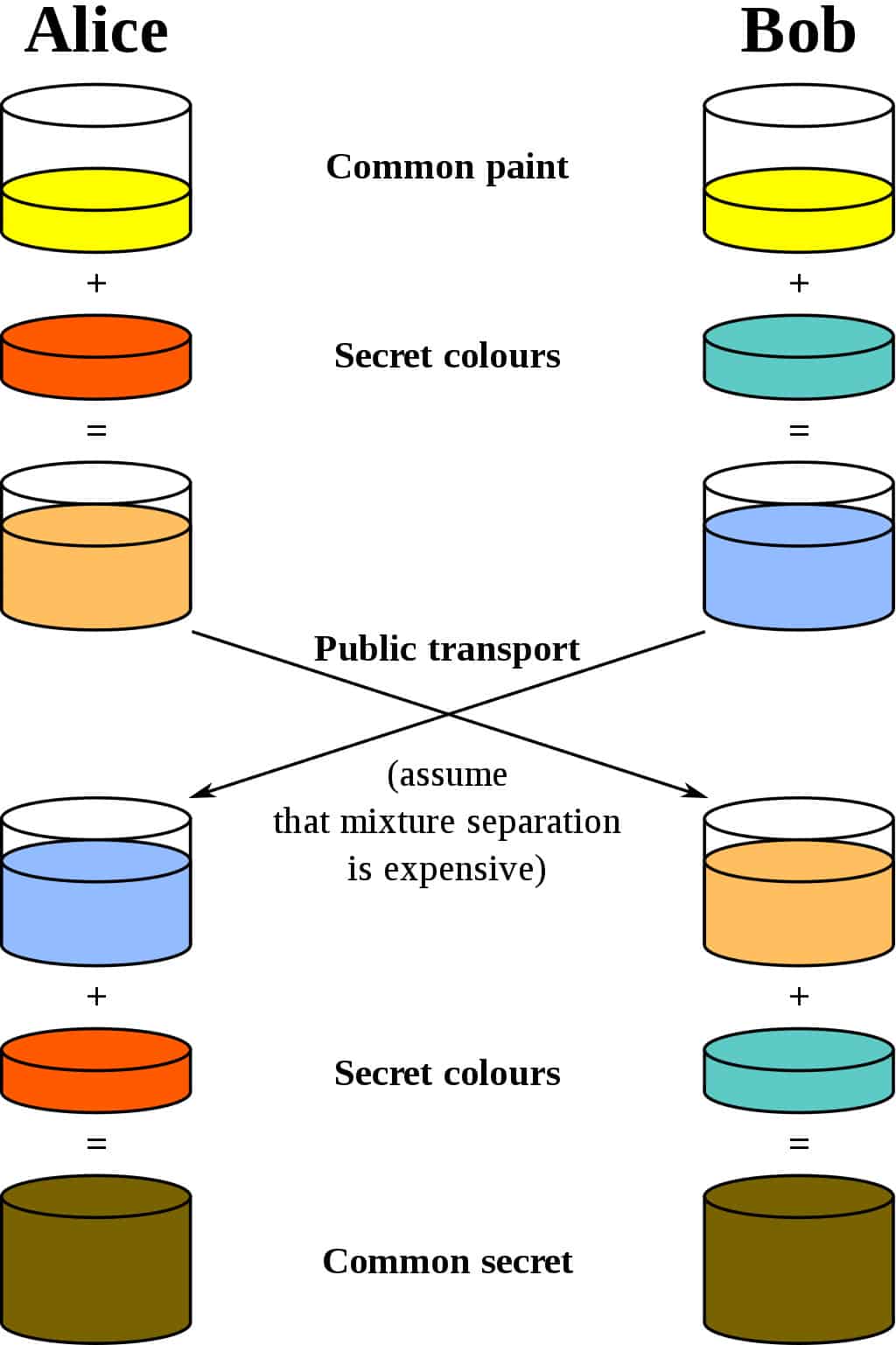
この DH 鍵共有のアルゴリズムはしばしば Fig 2. のようなインクの混ぜ合わせによって双方で共通の色を作る操作で説明されている。
- \(p, g\) を 2 者間で取り決める (これらは平文で公開されていても良い)。
- A: 秘密鍵 \(S_a \in \mathbb{Z}\) を決め、公開鍵 \(P_a = g^{S_a} \bmod p\) を計算して B に渡す。
- B: 秘密鍵 \(S_b \in \mathbb{Z}\) を決め、公開鍵 \(P_b = g^{S_b} \bmod p\) を計算して A に渡す。
- A: 秘密鍵 \(S_a\) と B の公開鍵 \(P_b\) を使って \(P_b^{S_a} = (g^{S_b})^{S_a} \bmod p\) を計算する。
- B: 秘密鍵 \(S_b\) と A の公開鍵 \(P_a\) を使って \(P_a^{S_b} = (g^{S_a})^{S_b} \bmod p\) を計算する。
- A と B は \(g^{S_a S_b} \bmod p\) という共通の値を共有した。
\(p, g\) を知っている攻撃者が A の公開鍵 \(P_a\) を盗聴したとしても DLP により秘密鍵 \(S_a\) を算出することは困難である。従って \(P_a\) と \(P_b\) を盗聴できても共通の値 \(g^{S_a S_b}\) を算出することはできず \(g^{S_a S_b}\) は A と B のみが知り得る情報である。
\(g\), \(p\), \(g^a \bmod p\), \(g^b \bmod p\) が与えられたとき \(g^{ab} \bmod p\) を求めることを DH 問題 (Diffie-Hellman problem) と呼び、DH 問題が現実的なコンピュータの計算能力で解くことが困難であるという仮定を CDH 仮定 (computational Diffie-Hellman assumption) と呼ぶ。したがって "攻撃者は CDH 仮定の下で \(g^{S_a S_b}\) を得ることが困難である" という表現が正確である。
一般に DH 鍵共有ではセキュリティを確保するためにモジュラス \(p\) は少なくとも 2048 ビット長であることが推奨されるが、ベース \(g\) は小さな値でもよい。
DH 鍵共有は攻撃者の盗聴に対しては耐性を持つが、交換する公開鍵のすり替えによって中間者攻撃が可能である。このような Anonymous Diffie-Hellman は安全ではなく、通常は証明書付きの公開鍵を使用して通信相手の身元を検証できるように設計しなければならない。
ephemeral-DH と static-DH があり、static-DH は前方秘匿性 (forward secrecy; ある鍵共有セッションが解読されたとしても過去のセッションのいずれも解読できない性質) を持たないため TLS では非推奨 (あるいは廃止) とされている。
 ElGamal 暗号
ElGamal 暗号
ElGamal 暗号は 1984 年に考案された CDH 仮定に基づいた公開鍵暗号方式。公開鍵で暗号化した暗号文は秘密鍵でしか復号化できず、同じ平文に対して毎回異なる暗号文が生成される。
- 構成: 大きな素数 \(p\) と原始根 \(g \bmod p\) を選択して暗号スキームのパラメータとして公開する。
- 鍵生成: 秘密鍵 \(S_a \in \{0, \ldots, p-2\}\) をランダムに選択し、\(P_a = g^{S_a} \bmod p\) を公開鍵とする。
- 暗号化: 平文 \(m\) の暗号化を考える。まずランダムに \(b \in \{0,\ldots,p-2\}\) を選択し、暗号スキームのパラメータ \(p\), \(g\) を使って \(B = g^b \bmod p\) を計算する。次に公開鍵 \(P_a\) から \(C = m P_a^b \bmod p\) を計算し \((B,C)\) を暗号文とする。
- 復号化: 秘密鍵 \(S_a\) と暗号文 \((B,C)\) より、以下のように \(p\), \(g\), \(S_a\), \(b\) を打ち消すことで元の平文 \(m\) を復元することができる。\[ \begin{equation} \frac{C}{B^{S_a}} = \frac{m P_a^b \bmod p}{(g^b)^{S_a} \bmod p} = \frac{m g^{bS_a} \bmod p}{g^{bS_a} \bmod p} = m \label{decrypt} \end{equation} \]
CDH 仮定より暗号文 \((B,C)\) から \(S_a\), \(b\), \(m\) を推測することは困難であり、また \(b\) のランダム性により同一の \(m\) であっても生成される暗号文は毎回違うものとなる。ただし式 (\(\ref{decrypt}\)) より、暗号文 \((B,C)\) を得た中間者が \((B,nC)\) にすり替えた場合、復号者は \(m\) ではなく \(nm\) を "正しく" 得ることとなる。つまり、ElGamal 暗号は中間者から通信内容を秘匿するが内容を操作することが可能であり頑強性や非展開性が欠落している。このため実用面ではあえて利用することはない。
 DSA 署名
DSA 署名
DSA (digigal sigunature algorithm) は欠点のあった ElGamal 署名の改良版として開発され 1993 年に標準化された電子署名アルゴリズム。RSA より小さな鍵や署名サイズで同等の安全性を保つことができる。
- 構成: ハッシュ関数 \(H\) と DH パラメータとなる大きな素数 \(p\)、およびハッシュ関数の出力と同じサイズの \(q\) を取り決める。
- 鍵生成: 生成元 \(g\) は \(g^q \equiv 1 \bmod p\) であり、\(p-1\) は \(q\) で割り切れるとする。\(0 \lt S_a \lt q\) となる秘密鍵 \(S_a\) をランダムに選択し、公開鍵を \(P_a = g^{S_a} \bmod p\) とする。
- 署名: 整数 \(k\) をランダムに選択する。メッセージ \(m\) に対して署名 \((r,s)\) を \(q\) を法として以下のように算出する (\(r=0\) または \(s=0\) の場合は \(k\) を再選択する)。\[ \begin{eqnarray*} r & = & g^k \bmod p \\ s & = & \frac{H(m)+rS_a}{k} \end{eqnarray*} \]
- 検証: まず \(0 \lt r \lt q\), \(0 \lt s \lt q\) でなければ署名は無効である。次に \(q\) を法として \[ \begin{eqnarray*} w & = & \frac{1}{s} = \frac{k}{H(m)+rS_a} \\ u_1 & = & w H(m) \\ u_2 & = & rw \\ v & = & g^{u_1} P_a^{u_2} \bmod p \end{eqnarray*} \] を算出し、\(g^{u_1} P_a^{u_2} = g^{wH(m)} g^{wrS_a} = g^{w(H(m)+rS_a)} = g^k\) より \(v = (g^k \bmod p) \bmod q = r\) が成り立つことから \(v = r\) であれば署名は有効である。
 Schnorr 署名
Schnorr 署名
Schnorr 署名は 1989 年に開発された離散対数問題に基づく署名アルゴリズム。DSA に存在する除算ステップが存在しないため演算はより効率的である。2008 年に特許が切れている。
- 鍵生成: 秘密鍵 \(S_a \in \mathbb{Z}_q\) をランダムに選択し、公開鍵を \(P_a = g^{-S_a}\) とする。
- 署名: 整数 \(r \in \mathbb{Z}_q\) をランダムに選び \(c = H(m,g^r)\), \(y=r+cS_a \bmod q\) を計算する。署名を \(\sigma=(c,y)\) とする。
- 検証: \(c=H(m,g^y P_a^c)\) であれば署名は有効である。
ランダムオラクルモデルにおいて離散対数仮定の元で選択メッセージ攻撃に対して安全であることが証明されている。
複数の署名を一つの署名にまとめるマルチ署名のアルゴリズムが存在する。Bitcoin ではこのマルチ署名を使用してブロックサイズを削減する提案が行われていたが現在は音沙汰がない。
参考文献
- 辻井重男, 笠原正雄, 有田正剛, 境隆一, 只木孝太郎, 趙晋輝, 松尾和人, "暗号理論と楕円曲線", 森北出版 (2008)
- J.A. ブーフマン, "暗号理論入門 原書第3版, 丸善出版 (2012)
- 光成滋生, "クラウドを支えるこれからの暗号技術", 秀和システム (2015)
- [HoECC05] Henri Cohen, Gerhard Frey, Roberto Avanzi, Christophe Doche, Tanja Lange, Kim Nguyen, Frederik Vercauteren, "Handbook of Elliptic and Hyperelliptic Curve Cryptography", Chapman and Hall/CRC; 1版 (2005)