セキュリティ
\( \def\vector#1{\boldsymbol{#1}} \)

Verifiable Random Function

Takami Torao #VRF #暗号抽選 #暗号選挙
  • このエントリーをはてなブックマークに追加

概要

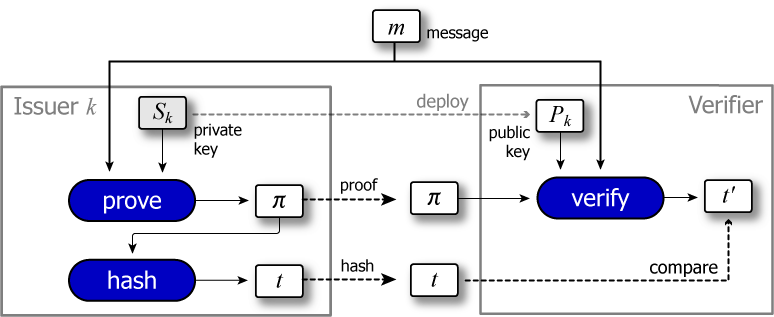
VRF (verifiable random function) は公開鍵ペアを使用する暗号学的ハッシュ関数である。VRF 関数は秘密鍵を使ってある入力値に対するハッシュ値を算出することができる。加えて、第三者がその公開鍵を使って、受信したハッシュ値が本当にその秘密鍵を使って生成されたものであるかを検証することができる。

Fig 1. How VRF works.

VRF によって生成される証明 \(\pi\) とハッシュ値 \(t\) はメッセージ \(m\)、秘密鍵 \(S_k\) に対して固有の値となるため、たとえ発行者であっても意図的に値を操作することはできない。

Table of Contents

  1. 概要
  2. アルゴリズム
    1. 証明とハッシュ値の生成
    2. ハッシュ値の検証
    3. セキュリティ
  3. 指名型暗号抽選スキーム
    1. 設定
    2. アルゴリズム
    3. Pros. and Cons.
    4. 複数抽選券に拡張
  4. P2P 型暗号抽選スキーム
    1. 設定
    2. アルゴリズム
    3. Pros. and Cons.
    4. 複数抽選券に拡張
  5. 他の暗号技術との比較
  6. 参考文献

アルゴリズム

VRF は証明の生成、ハッシュ値の生成、証明の検証の 3 つの関数で構成される。

証明とハッシュ値の生成

ある主体 \(k\) が保持する鍵ペアの秘密鍵を \(S_k\)、公開鍵を \(P_k\) とする。VRF 関数 \({\rm prove}()\) はあるメッセージ \(m\) に対する証明 (proof) \(\pi\) を算出し、さらに \({\rm hash}()\) は証明に対するハッシュ値を算出する。\[ \left\{ \begin{array}{lcl} \pi & = & {\rm prove}(S_k, m) \\ t & = & {\rm hash}(\pi) \end{array} \right. \] \(m\) に対して \(S_k\) を使って算出した証明値 \(\pi\) は \(k\) にしか作り得ない値と考えることができる。同様に \(t\) も \(k\) しか作り得ない暗号的ハッシュ (暗号論的疑似乱数) と考えられる。また \(\pi\) や \(t\) は入力に対して一意であるため \(k\) が意図的にそれらの値を調整することはできない。

ハッシュ値の検証

VRF には公開鍵 \(P_k\)、メッセージ \(m\) と証明 \(\pi\) からも \(t\) と同じハッシュ値を生成できるという特徴がある。つまり公開鍵 \(P_k\) を持っていれば、渡された証明 \(\pi\) やハッシュ値 \(t\) が本当に \(k\) によってメッセージ \(m\) に基づいて生成されたものかを検証することができる。\[ t' = {\rm verify}(P_k, m, \pi) \] もし \(\pi\) が \(S_k\) と \(m\) から生成されたものであれば \(t=t'\) となるし、そうでなければ \(t \ne t'\) や算出不能となる。

セキュリティ

攻撃者は公開鍵 \(P_k\) といくつかの \((m, t)\) セットを持っていたとしても、それらから秘密鍵を推測することができないし、\(k\) に問い合わせることなく未知の \(m'\) に対するハッシュ値 \(t'\) を推測することもできない。つまり VRF はオフライン攻撃やレインボーテーブル攻撃 (原像攻撃) の耐性を持っている。

VRF の生成するハッシュ値 \(t\) は暗号論的疑似乱数と同じ特性を持ち、例えば通信内容が暴露したとしてもビットの偏りからハッシュ値のフィールドがどこにあるかを特定することを困難にしている (副次的に、VRF のハッシュ値は一様乱数として使用することができる)。IRTF Draft [2] で策定されている ECVRF-EDWARDS25519-SHA512-ELL2 といった暗号スイートの末尾 -TAI (try-and-increment [4]) や -ELL2 (elligator [5] ) が楕円曲線点を一様乱数と区別が付かないようにするアルゴリズムを示している。

指名型暗号抽選スキーム

VRF を使った公平でセキュリティの高い抽選や宝くじシステムを設計してみよう。説明を簡略化するため参加者 1 人あたり 1 枚の抽選券を持っているとする (1 枚以上の場合は後述する)。参加者数 (=総抽選券枚数) を \(N\)、VRF 乱数の範囲を \(0 \ge t \gt 1\) とする。

Fig 2. Designated Cryptographic Lottery Scheme

この指名型抽選は信頼済みのディーラー (抽選会の運営団体) が当選者を指名する。VRF を使用することでディーラーが意図的に乱数を操作していないことを参加者が検証することができる。

設定

  1. ディーラーは鍵ペア \(S_k\), \(P_k\) を持っており、公開鍵 \(P_k\) はすべての参加者に共有されている。
  2. 参加者は ID 等で決定性のあるソートが可能であり、参加者リストはすべての参加者に共有されている。
  3. シード (メッセージ) \(m\) は誰でも知りえるが、ディーラーが推測したり操作することができない。

アルゴリズム

指名型抽選はランダムサンプリングに基づいた抽選アルゴリズムである。

  1. ディーラーは秘密鍵 \(S_k\) とシード \(m\) を使って証明 \(\pi\) と乱数 \(t\) を生成し参加者に通知する。
    val pi = vrf_prove(Sk, m)
val t = vrf_hash(pi)
  2. 参加者はディーラーの公開鍵 \(P_k\) とシード \(m\)、証明 \(\pi\) を使用して乱数 \(t\) を検証し、当選者を認識する。
    if(vrf_verify(Pk, m, pi) != t) {
	abort()
}
val winner = participants[floor(t * N)]

ここで、ディーラーがすぐに当選者を公表するか、先に当選者のみに通知するかはアプリケーションの要件によって考慮する必要がある。

  1. 当選者を公表する場合:
    1. ディーラーは \(\langle m, \pi, t\rangle\) をブロードキャストする。
    2. 各参加者は \(\pi\) と \(t\) が \(m\) に基づいてディーラーによって生成されたものであることを検証する。
    3. 各参加者は参加者リストから \(\lfloor t \times N \rfloor\) 番目の参加者を当選者と判断する。

    この方法は単純で公明だが、匿名性が低く、当選者が当選した権利を行使する前に悪意のある参加者からの攻撃を受けて権利の行使を妨害される可能性がある。

  2. 当選者のみに通知する場合:
    1. ディーラーは参加者リストから \(\lfloor t \times N \rfloor\) 番目の参加者を当選者と判断する。
    2. ディーラーは \(\langle m, \pi, t\rangle\) を当選者のみに送信する。
    3. 当選者は \(\pi\) と \(t\) が \(m\) に基づいてディーラーによって生成されたものであることを検証する。
    4. 当選者はディーラーと同じ方法で自分が当選者であることを検証する。
    5. 当選者は当選の権利を行使する。
    6. 当選者またはディーラーは、当選権の行使後に \(\langle m, \pi, t\rangle\) をブロードキャストし、他の参加者は正当な抽選であったことを検証する。

    これは抽選結果を検証可能にするため最終的に当選者は公表されるが、当選権利を行使するまでは公表されない方法である。抽選が失敗したとき、当選者以外の参加者は、ディーラーが故障したのか当選者が故障したのかを判断することができない。

このような抽選を継続的に行う場合、あるラウンド \(i\) での当選者が次のラウンド \(i+1\) でのディーラー役を担当しても良いだろう。この場合、次のラウンドのシードには \(m_{i+1} = {\rm sha256}(m_i || r || i)\) などを用いることができる (\(||\) は連結を表す)。

Pros. and Cons.

  • 乱数を発生させるディーラーは参加者より早く当選者を知りえてしまう点が公平性の解釈で不利と言える。例えば、ディーラーに不利な参加者が当選した場合に抽選そのものを無効にするかもしれない。
  • シードが既に暗号的乱数の性質を持っているのであれば、ディーラーが VRF を使用して乱数を生成する必要性は薄い。

複数抽選券に拡張

上記は単純化のため参加者 1 人あたり 1 つの抽選券を想定していた。ここで各参加者が 0 枚以上の抽選券を持つことができる場合を考えてみよう。

参加者の総数を \(K\)、ある参加者 \(k=1,2,\ldots,K\) の保有する抽選券の枚数を \(n_k\)、抽選券の総発行枚数を \(N=\sum_{i=1}^K n_i\) としたとき、それぞれの参加者の当選確率は \(p_k = \frac{n_k}{N}\), \(\sum_{i=1}^K p_i = 1\) である。これはカテゴリカル分布 \(P(x;\vector{p})\) に従う確率分布とみなすことができる。つまり以下の条件を満たす \(x\) が当選者である。\[ \left. \begin{array}{ll} 0 & \ \ {\rm if } \ \ x=1 \\ \sum_{i=1}^{x-1} p_i & \ \ {\rm Otherwise} \end{array} \right\} \le t \lt \sum_{i=1}^x p_i \] これは単純な累積和法を使用したランダムサンプリングと等しい。

例: A, B, C がそれぞれ 1 枚, 1 枚, 2 枚の抽選券を持っているとすると、それぞれの当選確率は \(p_i\) は 0.25, 0.25, 0.5 である。ディーラーの乱数が 0.20 のとき A、0.31 のとき B、0.72 のとき C が当選者に該当する。

P2P 型暗号抽選スキーム

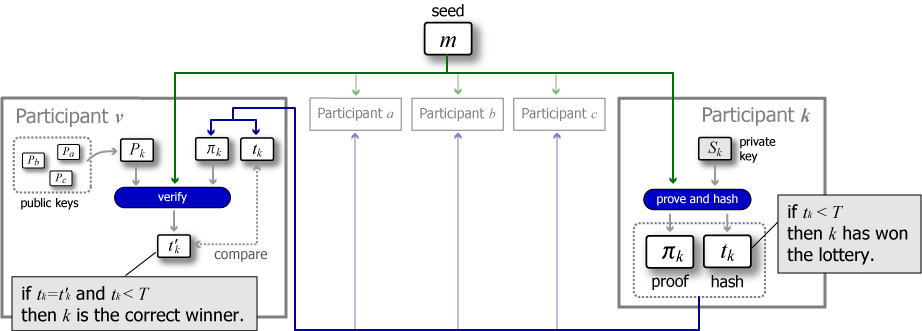
このスキームは各参加者が各自のプライベートな環境で VRF 乱数を生成し自分が当選者かを判断する。乱数は各参加者の秘密鍵 \(P_k\) とシード \(m\) によって決定するため意図的に操作することはできない。また、他の参加者の抽選結果はそれが公表されるまで知り得る方法はない。

Fig 3. P2P Cryptographic Lottery Scheme

このスキームは特定のしきい値 \(T\) より小さい VRF 乱数を引き当てた参加者を当たりと見なしている。例えば \(N=1000\) のうち概ね \(n=10\) 程度を当選させたい場合は \(T=0.01\) を設定する。この場合、当選者数が正確に \(n=10\) とは限らないことに注意。当選者数は \(n=10\) を中心としたガウス分布となるだろう。

設定

  1. 全ての参加者は鍵ペア \(S_k\), \(P_k\) を持っており、公開鍵 \(P_k\) は全ての参加者に共有されている。
  2. 参加者は公開鍵バイナリ等を使った決定性のあるソートが定義されている。
  3. シード (メッセージ) \(m\) はどの参加者でも知りうる。
  4. 当選しきい値 \(0 \le T \le 1\) が決められて共有されている。

アルゴリズム

各参加者 \(k\) がそれぞれ自身の秘密鍵 \(S_k\) とシード \(m\) から証明 \(\pi\)、乱数 \(t\) を計算し、その乱数がしきい値 \(T\) より小さければ自分が当選したと判断する。当選者はその証明と共に権利を行使し、検証者に \(\langle m, \pi, t \rangle\) を送信する (全ての参加者が検証する場合は全ての参加者に)。

Pros. and Cons.

  • ディーラーが不要であるため P2P 環境に適している。
  • 抽選時点での参加者数は決定的でなければならない。
  • 確率的な抽選であるため、結果として当選する参加者の数を正確に予測することができない。

複数抽選券に拡張

各参加者が 0 枚以上の抽選券を持つことができるケースを考える。ある参加者 \(k\) の保有する抽選券の枚数を \(n_k\)、抽選券の総発行枚数を \(N=\sum_{i=1}^K n_i\) とする。

総発行数 \(N\) のうち \(w\) 枚程度を当選させたい場合、抽選券 1 枚あたりに設定される当選確率は \(p=\frac{w}{N}\) である。つまり、参加者 \(k\) は当選確率 \(p\) の抽選券を \(n_k\) 枚持っており、抽選時に自身が生成した VRF ハッシュ値 \(t\) を使って何枚の当選券が含まれているかを求める (これは表が出る確率 \(p\) のコインを \(n_k\) 枚投げて表が出た個数を求める問題と同じである)。当選券枚数 \(x=\{0,1,\ldots,n_k\}\) に対する確率分布は二項分布 \(P(x)\) に従う。\[ \begin{eqnarray*} P(x;n_k,p) & = & \left(\begin{array}{c} n_k \\ x \end{array} \right) p^x (1-p)^{n_k-x} \\ & = & \frac{n_k!}{x! \ (n_k-x)!} \ p^x (1-p)^{n_k-x} \end{eqnarray*} \] \(0\le t \lt 1\) の一様乱数 \(t\) を特定の確率分布に従う乱数に変換するには逆関数サンプリングを行えば良い。つまり以下の条件を満たす \(x\) が参加者 \(k\) の持つ当選券の枚数である。\[ \sum_{i=0}^x P(i;n_k,p) \le t \lt \sum_{i=0}^{x+1} P(i;n_k,p) \]

この方法は 1 人の参加者が 2 枚以上の当選券を手にしている可能性があることに注意。

例: この方法で\(N=100\) 枚中おおむね \(w=5\) 枚が当たる抽選を行う場合について考える。抽選券 1 枚当たりの当選確率は \(p=\frac{5}{100}=0.05\) である。ある参加者 A は \(n_a = 2\) 枚の抽選券を持っている。つまり、\(P_a(0)=0.9025\), \(P_a(1)=0.095\), \(P_a(2)=0.0025\) である。一様乱数が \(t_a=0.5\) だった場合は 0 枚、\(t_a=0.995\) だった場合は 1 枚、\(t=0.998\) だった場合は 2 枚の当選券を持っていると見なすことができる。

参加者 \(k\) の公開鍵 \(P_k\) と抽選券保有枚数 \(n_k\) が共有されているなら、当選者が \(\langle m, \pi, t\rangle\) をブロードキャストすれば、当選者 \(k\) が当選枚数 \(x\) を保有していることを他の参加者が検証することができる。

他の暗号技術との比較

個人的な意見として VRF は以下の暗号技術との類似した特徴があると考えている。VRF を検討するとき、これらの技術を使った方が有利である可能性を考慮する必要があるだろう。

HMAC

HMAC は共有鍵 \(S\) を用いてメッセージ \(m\) に対するハッシュ値を算出する機能である。\(m\) に対する同一のハッシュ値は同一の鍵 \(S\) でしか生成し得ないことから、メッセージを送受信する主体の双方が共有鍵 \(S\) を共有していれば MHAC を使ってメッセージが改ざんされていないかを検証することができる。VRF は HMAC の共有鍵を公開鍵に拡張した概念と言える。

電子署名

\({\rm prove}()\) を署名生成、\({\rm hash}()\) を一般的なハッシュアルゴリズムとすると、電子署名はメッセージ \(m\) に対する秘密鍵 \(S_k\) による証明 \(\pi\) と考えることができる。これで VRF と類似した機能を構築することができるだろう。ただ、この方法は VRF より計算量が多く非効率的らしい。VRF が実装されていない環境での代替手段に使えるかもしれないのでここに書き留めておく。

VRF を使用することでワンタイムパスワードのようなスキームを考えることができるが、本人認証 (秘密鍵 \(S_k\) の所有確認) については一般的なチャレンジ/レスポンス認証や電子署名などの方法で行う方が良いだろう。VRF の特徴は意図的に操作されていない乱数を生成することである。

参考文献

  1. Silvio Micali, Michael Rabiny, Salil Vadhan (1999) Verifiable Random Functions (日本語訳)
  2. Verifiable Random Functions (VRFs) draft-irtf-cfrg-vrf-05 (日本語訳)
  3. Yossi Gilad, Rotem Hemo, Silvio Micali, Georgios Vlachos, Nickolai Zeldovich (2017) Algorand: Scaling Byzantine Agreements for Cryptocurrencies (日本語訳)
  4. Dan Boneh, Ben Lynn, and Hovav Shacham. Short signatures from the weil pairing. J. Cryptology, 17(4):297–319, 2004.
  5. Bernstein, D. J., Hamburg, M., Krasnova, A., Lange, T. Elligator : elliptic-curve points indistinguishable from uniform random strings. Cryptology ePrint Archive; Vol. 2013/325. IACR, 2013.