TLA⁺入門2: 独立した 2 変数のシステム

概要

このページでは TLA⁺ の例として時相論理演算子を扱う。

Table of Contents

1. 概要
2. :
   1. 例: 逐次処理
      1. TLA+ での表現

:

前述の TickTack システムは単一の変数だけだったため単純に状態変化をステップとみなすことができた。しかし 2 つ以上の独立した状態変数で構成されるシステムではある値が変化したときに別の値が変化しているとは限らない。このようなシステムでは特定の状態変数に対して変化しないステップを仕様として許可する必要がある (このような状態変数が変化しないステップをスタッターステップ (stuttering step) と呼ぶ)。

TickTack システムを少し拡張して時刻のみを表示する時計について考える (これは Specifying Systems [1] の最初の例と同じ)。時刻 \(hr\) は 1 から 12 のいずれかの数値であり、表示の切り替わり (ステップ) には時刻が加算され 12 を超えるケースに限り 1 となる。したがって初期状態と次の状態の 2 つのアサーションは以下のように表すことができる。\[ \begin{eqnarray*} {\it HCinit} & \ldef & hr \in \{1, \ldots, 12\} \\ {\it HCnxt} & \ldef & hr' = hr + 1 \ \mbox{if} \ hr \ne 12 \ \mbox{else} \ 1 \end{eqnarray*} \] ここで時相論理演算子 (temporal logic operator) の Globally を導入し、\(\globally F\) を \(F\) が常に true であることを主張するアサーションとする。つまり \(\globally {\it HCnxt}\) は動作のすべてのステップで \({\it HCnxt}\) が true であるというアサーションである。したがって式 (\(\ref{hc_def1}\)) はこの動作の全てを記述している仕様である。\[ \begin{equation} {\it HCinit} \land \globally{\it HCnxt} \label{hc_def1} \end{equation} \]

時計が独立した単独のシステムであればこの仕様の記述は適切である。ただし時計がシステムの一部で、例えば気温と同時に表示されるようなケースでは、時刻を表す \(hr\) と温度を表す \(tmp\) の 2 つの変数で表示される。この場合、温度の変化がありながら時刻は変化していないという表示の切り替わりケースがあることから \(hr\) を変更しないステップを許可する必要がある。\[ {\it HCinit} \land \globally ({\it HCnxt} \lor (hr' = hr)) \] このようなステップをスタッターステップ (stuttering step) と呼ぶ。時計の仕様は \({\it HCnxt}\) とスタッターステップを許可する必要がある。TLA では \({\it HCnxt} \lor (hr'=hr) \equiv [{\it HCnxt}]_{hr}\) と書くためよりシンプルに式 (\(\ref{hc_def2}\)) のように書くことができる。\[ \begin{equation} {\it HC} \ldef {\it HCinit} \land \globally [{\it HCnxt}]_{hr} \label{hc_def2} \end{equation} \] この仕様では時計がある時刻を示したあとに永久にスタッターステップを繰り返す (つまり時計が止まる) ことを許容している点に注意。

時間である \(hr\) に小数が付加されたり無理数や虚数になることはないため、\({\it HC} \Rightarrow \globally {\it HCinit}\) はあらゆる状況で成り立たなければならない。あらゆる状況で成り立つ時相式は定理 (theorem) と呼ばれる。

例: 逐次処理

The TLA+ Video Course で例示しているプログラムを使用して説明する。以下のようなプログラムは:

int i = 0;
void main(){
  i = someNumber();  // pc = "start"
  i += 1;            // pc = "middle"
}

仕様化された数式および TLA+ として以下のように表現することができる。これは元のプログラムとよく似ているが、プログラムが実行を表しているのに対して、仕様化された数式および TLA+ はステートマシンの状態が仕様に準拠しているか否かの true/false のみを表していることに注意。ここで各ステップは TLA+ の慣習として変数 pc を用いて識別している。

Init == (pc = "start") /\ (i = 0)
Next == \/ /\ pc = "start"
           /\ i' \in 0..1000
           /\ pc' = "middle"
        \/ /\ pc = "middle"
           /\ i' = i + 1
           /\ pc' = "done"

変数 x は \(x\) の現在の値、それにプライムが付いた変数 x' は \(x\) の次の値をそれぞれ表している (つまり x' として表されている変数は次のステップでは x として現れる)。

AND, OR はそれぞれ数学記号 \(\land\) と \(\lor\) に倣って /\ と \/ で表す。これらは従来の数式のように二項演算子として表記する以外にリストのように書くこともできる。\(\land\) と \(\lor\) はともに可換であり左右のオペランドを交換できる。

集合と包含 \(x \in \{0,\ldots,100\}\) は x \in 0..100 のように表す。

ステートマシンに基づく TLA+ の記述は UML の状態遷移図と親和性が良い。状態遷移図としては Fig 1 のように表すことができる。

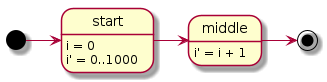
TLA+ で逐次処理を記述するとき 1) 実行中の位置を保持する状態変数を導入し (変数名は慣習的に pc とする)、2) 各ステップごとに状態チェックを定義し、3) 最終的に仕様は \({\it Init} \ \cap \ \globally [{\it Next}]_x\) の形式になる。しかし、現実問題として全てのステップにユニークな名前をつけることは煩雑な作業である。これらの 3 つの特徴を DSL 化したものが PlusCal である。

TLA+ での表現