$ \def\ldef{\ \ :=\ } $ $ \def\rdef{\overset{\triangle}{=}} $ $ \def\globally{□} $ $ \def\eventually{◇} $

TLA⁺ と PlusCal

2021年3月14日 TLC2 #TLA+ #TLC #PlusCal

概要

TLA⁺ (temporal logic of actions plus; 1999年) と PlusCal (2009年) は共に並行処理と分散システム向けに設計された仕様記述言語 (高レベルモデリング言語)。システム設計やアルゴリズムなどの重要で危険度の高い部分のエラーを定性的に検出することを目的としている。

先に発表された TLA+ は振る舞いの時相理論、つまり有限状態機械 (finite state machine) の状態遷移を観点とした仕様記述向けに設計されている。しかし一般的なプログラミング言語の逐次処理や並行処理の構造を TLA+ で記述すると多くのボイラープレートが必要となる。PlusCal はそのようなボイラープレートを宣言化して省略し、より逐次処理の観点で記述できるようにした DSL である (最終的に TLA+ にトランスパイルされ TLC で検証される)。

このため並行システムの仕様記述を目的とするのであれば PlusCal が向いているが、モデル検証時のトラブルを解消するためには基本的な TLA+ の知識も必要となる (言い換えれば、トランスパイル結果の TLA+ は頻出のボイラープレートばかりであるため PlusCal を主軸に修習していても基本的な TLA+ の作法は覚えられるだろう)。

TLA+ も PlusCal も論文の理論説明に使う擬似コードのような十分に抽象化された設計を記述することを意図している。TLA+ の背後ではシステムを有限状態機械として検証していることから、UML の状態遷移図 (state diagram) と表現の親和性がよく、したがって TLA+ や PlusCal はシステムが想定する状態遷移を検証する道具と考えても良い。一方で、用意されている制御構造は非力でオブジェクト指向や関数型言語といった一般的なパラダイムも持たず (これらを導入すると状態遷移の全数テストがさらに複雑化するためだろう)、現実的で詳細なプログラムフローを記述することは難しい。

TLA+ や PlusCal は設計を抽象化する過程で設計者の主観や感覚の影響を大きく受けやすい。「TLA+ で証明済み」といった主張を盲信せず、どのような前提の下にどのようなケースが適用または省略されたか (省略した部分はどう実装することを想定しているか) を十分にレビューすべきである。

概要
1. TLA⁺
2. PlusCal
TLC モデルチェッカーの動作
環境設定と検証の実行
参照

TLA⁺

TLA⁺ はシステムやアルゴリズムを有限状態機械とみなし離散ベントの連続として抽象化する。TLA+ ではある状態から次の状態へのアトミックな変化を一つのステップとし、状態の変化の連続を振る舞い (behaviour) とする。どのような振る舞いが許可されるかは不変式やプロパティ、またはアサーションで検証される。全ての振る舞いとチェックを記述することは仕様化 (specify) である。

TLA+ の難しい点は機能要件をステートマシンに抽象化することと言われている。ステートマシンの振る舞いは 1) 取りうる初期状態と 2) 各状態が取りうる次の状態の 2 点で抽象化することができる (取りうる次の状態が存在しないときシステムは halt する)。TLA+ ではシステムの状態を表すために必要な変数とその初期状態、各変数間の関連と次の状態への遷移を定義することでその仕様を記述する。そして、システムがステップを進行するごとに "正しい状態" の要件を満たしているかをチェックして "正しく動く" ことを検証する。

TLA+入門1: TickTack

このページでは最初の TLA+ の例として、システム状態に 0 と 1 を交互にとる TickTack システムについて考える。

2021年2月5日(Fri) TLC2 #TLA+ #TLC

TLA+入門2: 独立した 2 変数のシステム

このページでは TLA+ の例として時相論理演算子を扱う。

2021年2月5日(Fri) TLC2 #TLA+ #TLC

翻訳: Summary of TLA+

2021年2月4日(Thu) #TLA+ #cheetsheet

PlusCal

PlusCal は逐次処理をモデル化することを目的に設計された仕様記述言語である。TLA+ の逐次処理向け DSL と言ったところで TLA+ から多くの構文や演算子を流用している。TLA+ と比較してより現実的なプログラミングに近い記述となっているが、背後では有限状態機械の挙動を探索し検査する点は同じである。

PlusCal の仕様は TLA+ のブロックコメント部分に記述する。PlusCal で記述された仕様は最終的に TLA+ にトランスパイルされて TLC でモデルチェックが行われる。

PlusCal の記述は JUnit のような単体テストフレームワークとよく似ていることから、一般的なプログラミング言語での単体テストに慣れているプログラマであればまず制御構文とアサーションを使った単体テストを作成するつもりで、背後でどのような状態遷移グラフが構築されているかを意識しながら取り掛かるのが近道だろう。その後にケース分岐を考慮して仕様を網羅する方法や、マルチプロセス間の非同期メッセージを検証する方法に進めば良い。

PlusCal入門1: hello, world

このページでは最初の PlusCal の例として hello, world と表示するプログラムをレビューし、その基本的な記述構造について考える。PlusCal での仕様記述や TLC 実行のための環境設定は環境設定と検証の実行を参照。…

2021年2月5日(Fri) TLC2 #TLA+ #TLC

PlusCal: データ構造と演算子

2021年3月8日(Mon) TLC2 #PlusCal #TLA+

PlusCal: 制御構造

このページではいくつかの例を使って PlusCal の基本的な制御構造を説明する。実行環境のセットアップは PlusCal を参照。

2021年3月8日(Mon) TLC2 #PlusCal #TLA+

PlusCal: 並行システムと非同期処理

このページでは PlusCal を使ってマルチプロセスやマルチスレッド、それらに伴う非同期処理といった並行処理を記述する方法について説明する。サンプルを実行するための環境セットアップは環境設定と検証の実行を参照。…

2021年3月9日(Tue) TLC2 #PlusCal #TLA+

PlusCal: 証明アプローチ

このページでは PlusCal を使って記述したシステムが正しいことをどのように証明するかについて説明する。サンプルを実行するための環境セットアップは環境設定と検証の実行を参照。

2021年4月8日(Thu) TLC2 #PlusCal #TLA+

翻訳: A PlusCal User's Manual

2021年3月8日(Mon) 2020年の論文 #PlusCal #TLA+

翻訳: The PlusCal Algorithm Language

2021年3月19日(Fri) 2009年の論文 #PlusCal #TLA+

翻訳: PlusCal/TLA+: An Annotated Cheat Sheet

PlusCal と TLA+ のリファレンスとして有用なチートシート。

2021年3月27日(Sat) 2019年の論文 #PlusCal #TLA+

TLC モデルチェッカーの動作

TLC は TLA+ (PlusCal からトランスパイルされた TLA+ を含む) の仕様記述を検証するプログラムである。スクリプト言語のようにインタープリターとして実行される。

変数定義域×組み合わせケースの自動化

TLC は VARIABLES で宣言された状態変数の定義域やプロセス進行状況、非決定論的な分岐など、システムが取りうるすべての組み合わせを自動で探索して検証する。

状態変数の定義域をどのように定義するかは TLC 検査のパフォーマンスに大きく影響する。例えば以下の例を実行すると 2G×2G=$4.6\times 10^{18}$ のケース全てに対して $x+y \ge 0$ の検証を試みるが、当然ながら計算量の爆発によって今世紀中に TLC 検査が終わることはないだろう。

---- MODULE CombinationalExplosion ----
EXTENDS Integers, TLC
(* --algorithm CombinationalExplosion
variables x \in 0..2147483647;
          y \in 0..2147483647;
begin
  A: assert x + y >= 0;
end algorithm; *)
====

このような整数型の全値を定義域とするような検査の方法は TLC では現実的ではない。設計をより抽象化して本当に意味のある状態の定義のみとなるよう見直すか (実際 2,147,483,647 個もの状態が個別に意味を持つことは稀である)、全数テストを諦めてコーナーケースといくつかの代表値のみを検査対象とするように修正する必要がある。

状態変数の記憶による実行最適化と停止

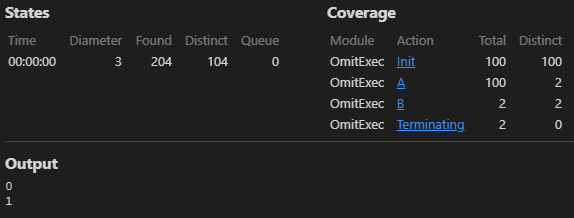
TLC はステップごとに状態変数を記録していて、ある過程を終えた後の状態変数が過去に検証済みであればそれ以上の実行を省略する。例えば以下の例では $x \in \{0,\ldots,99\}$ の定義域で開始するが、ステップ A を終えた時点で $x \in \{0,1\}$ の状態に収束することから、ステップ B 以降は $x=0$ と $x=1$ の 2 通りの検証が行われれば十分である。

Fig 1. 実行結果より、ステップ `A` が 100 ケース実行されているのに対して、ステップ `B` は 2 回しか実行されていないことが分かる。

この最適化をうまく使うと状態変数の数や取りうる状態の数を減らして TLC 検証の実行効率を改善することができる。やりすぎは逆効果だが、考慮すべき状態を削減することは設計をよりシンプルにするだろう。

この特性により、実装上は停止条件が存在しない仕様だとしても TLC の検査は停止することができる。実際のこの挙動は PlusCal の while 構文を参照。

状態変数はハッシュ値として記録されており、検証成功時に表示される Fingerprint collision probability とはその状態ハッシュが衝突している確率を示している。

状態変数の記憶によるバックトレース

単純な逐次処理を TLA+ や PlusCal を使って仕様を記述することは Python などの言語で unit-test を記述しているのとそれほど大きく変わることはない。むしろ形式仕様言語で記述できる程度に目的の仕様を過不足なく抽象化する過程が難しい点であって、その検証をどのような手段で行うかはそれほど重要な点ではないという考えもある。

しかし、一般的な言語のテストフレームワークが失敗条件と stack trace 程度しか報告しないのに対して、TLA+ や PlusCal がどのような状態遷移を経て失敗したかを報告するという点は設計者やプログラマにとって明らかに有用な機能の一つだろう。

例として機内食に提供するメニューの仕様について考える。ここでベジタリアンには野菜のみのメニュー、アレルギーを持つ人にはアレルギー食材を除いたメニューを提供しようとしている。この仕様は一見して正しく条件分岐しているように見えるが TLC 検査は失敗する。

Fig 2. Error Trace には失敗ケースでの各ステップの状態変数の推移が出力される。

Fig 2 の Error Trace にはラベル付けされた過程とその状態変数の推移が出力される。この例ではベジタリアンかつアレルギーありのケースでアレルギー食材である "beans" がメニューに含まれてしまっていることが分かる。

デッドロックの検出

TLC はすべてのプロセスが終了していないにもかかわらず進行可能なステップがなくなった状況をデッドロックとする。

環境設定と検証の実行

実際の TLA+, PlusCal を記述する前に、まず Visual Studio Code (vscode) の TLA+ 拡張機能を使用した TLA+ の記述と検証方法について説明する。TLA+ 拡張機能の詳細については公式サイトの Wiki を参照。この拡張機能は PlusCal にも対応している。

vscode 拡張機能のインストール

Visual Studio Code のサイトから vscode をダウンロードしてインストールし、拡張機能のマーケットプレイスから TLA+ の拡張機能を追加する。この記事では vscode を使用して説明を行う。

IntelliJ IDEA プラグインのインストール

IntelliJ IDEA でも vscode の TLA+ 拡張機能と同等のプラグインを利用することができる。PlusCal を使用する場合はソースコードを右クリックし [TLA+]-[Translate PlusCal] で TLA+ へトランスパイルし、[実行] で TLC を実行することができる。

仕様記述

vscode 上でプロジェクトを作成して HelloWorld.tla というファイルに TLA+ または PlusCal で仕様を記述する。ここで MODULE とファイル名は同じ名前にすることに注意。

---- MODULE HelloWorld ----
EXTENDS TLC
VARIABLES pc
Init == pc = "greeting"
Greeting == /\ pc = "greeting"
            /\ PrintT("hello, world")
            /\ pc' = "finish"
Termination == /\ pc = "finish"
               /\ UNCHANGED pc
Next == Greeting \/ Termination
====

---- MODULE HelloWorld ----
EXTENDS TLC
(* --algorithm HelloWorld
begin
  Greeting:
    print "hello, world";
end algorithm; *)
====

Example 5. TLA+ (左) と PlusCal (右) で記述した hello, world。

トランスパイル

PlusCal で記述した場合は [View]-[Command Palette...] メニューか CTRL+Shift+P を押して "TLA+: Parse module" を選択すると Example 6 のような TLA+ のコードにトランスパイルされる。同時にモデルファイルの HelloWorld.cfg も生成され、翻訳前の内容は HelloWorld.old に保存されてる。

TLC 検証

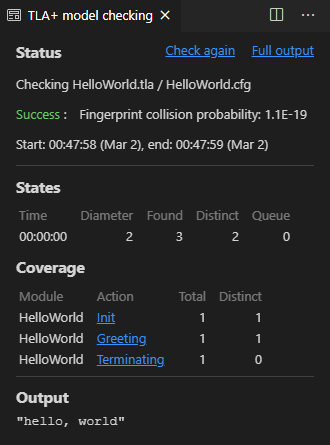
次に EXPLORER ペインで HelloWorld.tla ファイルを右クリックして "Check model with TLC" を選択すと TLC によるモデルチェックが実行されて結果が表示される (Fig 7)。

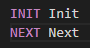
Fig 7. コンテキストメニューに表示されている "Check model with TLC" を選択すると TLC によりモデルのチェックが行われる。

ここで TLA+ の例でまだモデル HelloWorld.cfg が存在しない場合は Fig 8 のように誘導される。モデルファイルでは HelloWorld モジュールで使用する定数やデッドロック時の挙動などを指定できるが、ひとまずこの例では INIT (取りうる初期状態) と NEXT (各状態が取りうる次の状態) の定義とのマッピングのみを指定する。

TLC は TLA+ で記述された仕様に対して状態モデルのチェックを行うプログラムである (TLC は Java で実装されているためコマンドラインから Java を起動できるようにしておく必要があるかもしれない)。結果 Status 右上の "Full output" をクリックすると以下のような TLC 出力の詳細が表示される。

java.exe -cp "c:\Users\Takami Torao\.vscode\extensions\alygin.vscode-tlaplus-1.5.3\tools\tla2tools.jar" -XX:+UseParallelGC tlc2.TLC HelloWorld.tla -tool -modelcheck -coverage 1 -config HelloWorld.cfg

TLC2 Version 2.16 of 31 December 2020 (rev: cdddf55)
Running breadth-first search Model-Checking with fp 33 and seed 600503388950936924 with 1 worker on 24 cores with 7266MB heap and 64MB offheap memory [pid: 9856] (Windows 10 10.0 amd64, Oracle Corporation 11 x86_64, MSBDiskFPSet, DiskStateQueue).
Starting SANY...
Parsing file C:\Users\Takami Torao\...\HelloWorld.tla
Parsing file C:\Users\Takami Torao\AppData\Local\Temp\TLC.tla
Parsing file C:\Users\Takami Torao\AppData\Local\Temp\Naturals.tla
Parsing file C:\Users\Takami Torao\AppData\Local\Temp\Sequences.tla
Parsing file C:\Users\Takami Torao\AppData\Local\Temp\FiniteSets.tla
Semantic processing of module Naturals
Semantic processing of module Sequences
Semantic processing of module FiniteSets
Semantic processing of module TLC
Semantic processing of module HelloWorld
SANY finished.
Starting... (2021-03-13 22:12:55)
Computing initial states...
Finished computing initial states: 1 distinct state generated at 2021-03-13 22:12:56.
"hello, world"
Model checking completed. No error has been found.
  Estimates of the probability that TLC did not check all reachable states
  because two distinct states had the same fingerprint:
  calculated (optimistic):  val = 1.1E-19
The coverage statistics at 2021-03-13 22:12:56
<Init line 5, col 1 to line 5, col 4 of module HelloWorld>: 1:1
  line 5, col 9 to line 5, col 23 of module HelloWorld: 1
<Greeting line 6, col 1 to line 6, col 8 of module HelloWorld>: 1:1
  line 6, col 16 to line 6, col 30 of module HelloWorld: 3
  |line 6, col 16 to line 6, col 17 of module HelloWorld: 2
  line 7, col 16 to line 7, col 37 of module HelloWorld: 1
  line 8, col 16 to line 8, col 29 of module HelloWorld: 1
<Termination line 9, col 1 to line 9, col 11 of module HelloWorld>: 0:1
  line 9, col 19 to line 9, col 31 of module HelloWorld: 3
  |line 9, col 19 to line 9, col 20 of module HelloWorld: 2
  line 10, col 19 to line 10, col 32 of module HelloWorld: 1
End of statistics.
Progress(2) at 2021-03-13 22:12:56: 3 states generated (344 s/min), 2 distinct states found (229 ds/min), 0 states left on queue.
3 states generated, 2 distinct states found, 0 states left on queue.
The depth of the complete state graph search is 2.
The average outdegree of the complete state graph is 1 (minimum is 0, the maximum 1 and the 95th percentile is 1).
Finished in 526ms at (2021-03-13 22:12:56)

ここでは Success と表示されていることから HelloWorld システムが取りうる全ての状態で仕様を満たしていることがわかる。ただしこの hello, world の例は意味のある状態変数もアサーションも持たないため TLC での実行は単に hello, world を逐次実行したのと変わらない。PlusCal や TLA+ の一般的な記述では仕様の最後または処理の途中でアサーションを記述し、システムの状態変数が正しいことを検証する。

LaTeX 出力

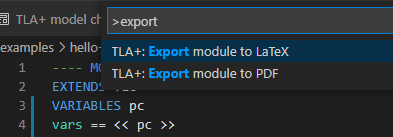
TLA+ で記述した場合は [View]-[Command Palette...] メニューまたは CTRL+Shift+P ショートカットを使って LaTeX または PDF に出力することができる。PDF 化には latex コマンドを求められるが、ローカルに LaTeX をインストールしていない場合は overleaf などのサイトにファイルの内容をコピーして生成することもできる。

Fig 9. LaTeX 形式で出力し PDF 化した "公式な表現の" TickTack システム仕様。

コマンドライン実行

vscode ディレクトリの tla2tools.jar を使って java コマンドから直接 TLC を起動することができる。最新版では簡易的な REPL も用意されているようなので将来的に使えるようになるかもしれない。

$ export TLA2TOOLS="$HOME/.vscode/extensions/alygin.vscode-tlaplus-1.5.3/tools/tla2tools.jar"

$ java.exe -cp "$TLA2TOOLS" tlc2.TLC -help

NAME

        TLC - provides model checking and simulation of TLA+ specifications - Version 2.16 of 31 December 2020


SYNOPSIS

        TLC [-h] [-cleanup] [-continue] [-deadlock] [-debug] [-difftrace] [-generateSpecTE [nomonolith]] [-gzip] [-nowarning] [-te
rse] [-tool] [-view] [-checkpoint minutes] [-config file] [-coverage minutes] [-dfid num] [-dump [dot actionlabels,colorize,snapsh
ot] file] [-fp N] [-fpbits num] [-fpmem num] [-maxSetSize num] [-metadir path] [-recover id] [-userFile file] [-workers num] SPEC
        TLC [-h] [-cleanup] [-continue] [-deadlock] [-debug] [-difftrace] [-generateSpecTE [nomonolith]] [-gzip] [-nowarning] [-te
rse] [-tool] [-aril num] [-checkpoint minutes] [-config file] [-coverage minutes] [-depth num] [-dump [dot actionlabels,colorize,s
napshot] file] [-fp N] [-fpbits num] [-fpmem num] [-maxSetSize num] [-metadir path] [-recover id] [-seed num] [-userFile file] [-w
orkers num] -simulate [file=X,num=Y] SPEC

DESCRIPTION

        The model checker (TLC) provides the functionalities of model checking
        or simulation of TLA+ specifications. It may be invoked from the command
        line, or via the model checking functionality of the Toolbox.

        By default, TLC starts in the model checking mode using breadth-first
        approach for the state space exploration.

OPTIONS

        -aril num
                adjust the seed for random simulation; defaults to 0
        -checkpoint minutes
                interval between check point; defaults to 30
        -cleanup
                clean up the states directory
        -config file
                provide the configuration file; defaults to SPEC.cfg
        -continue
                continue running even when an invariant is violated; default
                behavior is to halt on first violation
        -coverage minutes
                interval between the collection of coverage information;
                if not specified, no coverage will be collected
        -deadlock
                if specified DO NOT CHECK FOR DEADLOCK. Setting the flag is
                the same as setting CHECK_DEADLOCK to FALSE in config
                file. When -deadlock is specified, config entry is
                ignored; default behavior is to check for deadlocks
        -debug
                print various debugging information - not for production use

        -depth num
                specifies the depth of random simulation; defaults to 100
        -dfid num
                run the model check in depth-first iterative deepening
                starting with an initial depth of 'num'
        -difftrace
                show only the differences between successive states when
                printing trace information; defaults to printing
                full state descriptions
        -dump file
                dump all states into the specified file; this parameter takes
                optional parameters for dot graph generation. Specifying
                'dot' allows further options, comma delimited, of zero
                or more of 'actionlabels', 'colorize', 'snapshot' to be
                specified before the '.dot'-suffixed filename
        -fp N
                use the Nth irreducible polynomial from the list stored
                in the class FP64
        -fpbits num
                the number of MSB used by MultiFPSet to create nested
                FPSets; defaults to 1
        -fpmem num
                a value in (0.0,1.0) representing the ratio of total
                physical memory to devote to storing the fingerprints
                of found states; defaults to 0.25
        -generateSpecTE
                if errors are encountered during model checking, generate
                a SpecTE tla/cfg file pair which encapsulates Init-Next
                definitions to specify the state conditions of the error
                state; this enables 'tool' mode. The generated SpecTE
                will include tool output as well as all non-Standard-
                Modules dependencies embeded in the module. To prevent
                the embedding of dependencies, add the parameter
                'nomonolith' to this declaration
        -gzip
                control if gzip is applied to value input/output streams;
                defaults to 'off'
        -h
                display these help instructions
        -maxSetSize num
                the size of the largest set which TLC will enumerate; defaults
                to 1000000 (10^6)
        -metadir path
                specify the directory in which to store metadata; defaults to
                SPEC-directory/states if not specified
        -nowarning
                disable all warnings; defaults to reporting warnings
        -recover id
                recover from the checkpoint with the specified id
        -seed num
                provide the seed for random simulation; defaults to a
                random long pulled from a pseudo-RNG
        -simulate
                run in simulation mode; optional parameters may be specified
                comma delimited: 'num=X' where X is the maximum number of
                total traces to generate and/or 'file=Y' where Y is the
                absolute-pathed prefix for trace file modules to be written
                by the simulation workers; for example Y='/a/b/c/tr' would
                produce, e.g, '/a/b/c/tr_1_15'
        -terse
                do not expand values in Print statements; defaults to
                expanding values
        -tool
                run in 'tool' mode, surrounding output with message codes;
                if '-generateSpecTE' is specified, this is enabled
                automatically
        -userFile file
                an absolute path to a file in which to log user output (for
                example, that which is produced by Print)
        -view
                apply VIEW (if provided) when printing out states
        -workers num
                the number of TLC worker threads; defaults to 1. Use 'auto'
                to automatically select the number of threads based on the
                number of available cores.

TIPS

        When using the  '-generateSpecTE' you can version the generated specification by doing:
                ./tla2tools.jar -generateSpecTE MySpec.tla && NAME="SpecTE-$(date +%s)" && sed -e "s/MODULE SpecTE/MODULE $NAME/g"
 SpecTE.tla > $NAME.tla

        If, while checking a SpecTE created via '-generateSpecTE', you get an error message concerning
        CONSTANT declaration and you've previous used 'integers' as model values, rename your
        model values to start with a non-numeral and rerun the model check to generate a new SpecTE.

        If, while checking a SpecTE created via '-generateSpecTE', you get a warning concerning
        duplicate operator definitions, this is likely due to the 'monolith' specification
        creation. Try re-running TLC adding the 'nomonolith' option to the '-generateSpecTE'

参照

Leslie Lamport (2002), Specifying Systems.
Leslie Lamport (2020), A PlusCal User’s Manual P-Syntax Version 1.8.
LEARN TLA+

TLA+ と PlusCal

概要

Table of Contents

TLA+

TLA+入門1: TickTack

TLA+入門2: 独立した 2 変数のシステム

翻訳: Summary of TLA+

PlusCal

PlusCal入門1: hello, world

PlusCal: データ構造と演算子

PlusCal: 制御構造

PlusCal: 並行システムと非同期処理

PlusCal: 証明アプローチ

翻訳: A PlusCal User's Manual

翻訳: The PlusCal Algorithm Language

翻訳: PlusCal/TLA+: An Annotated Cheat Sheet

TLC モデルチェッカーの動作

変数定義域×組み合わせケースの自動化

状態変数の記憶による実行最適化と停止

状態変数の記憶によるバックトレース

デッドロックの検出

環境設定と検証の実行

vscode 拡張機能のインストール

IntelliJ IDEA プラグインのインストール

仕様記述

トランスパイル

TLC 検証

LaTeX 出力

コマンドライン実行

参照

TLA⁺ と PlusCal

TLA⁺