TLA+
例2:時相理論演算子 ::
\( \def\ldef{\ \ :=\ } \) \( \def\rdef{\overset{\triangle}{=}} \) \( \def\globally{□} \)

TLA+入門1: TickTack

Takami Torao TLC2 #TLA+ #TLC
  • このエントリーをはてなブックマークに追加

概要

このページでは最初の TLA+ の例として、システム状態に 0 と 1 を交互にとる TickTack システムについて考える。

Table of Contents

  1. 概要
  2. TickTack の抽象化
  3. 基本的な TLA+ の記述
  4. TLC 検証結果
  5. エラーの検出

TickTack の抽象化

TLA+ による仕様の構築は経験的に以下のような手順で行うと良い。

  1. 目的のシステムに必要な振る舞いを定義する。
  2. 振る舞いが機能するために必要な状態変数を定義する。
  3. 全ての振る舞いを初期状態 (Init) と次の状態 (Next) で記述する。
  4. 振る舞いが正しいことをチェックするアサーションを作成する。

まず最初に、この TickTack システムの要件は以下の一つの振る舞いで表すことができる。

システムは 0 と 1 の状態を交互にとる。

この振る舞いを表すためには 0 か 1 かどちらかの値をとる単一の状態変数があれば十分であろう。この状態変数を \(t\) とし、その初期状態は 0 または 1 のどちらでも許容できるため式 (\(\ref{init}\)) のように定義することができる。\[ \begin{equation} {\it Init} \ldef t \in \{0, 1\} \label{init} \end{equation} \]

TLA+ ではあるステップの状態変数を \(x\) としたとき、その変数の次のステップでの状態を \(x'\) (\(x\)-プライム) と表現する。言い換えると「\(x'\) はこのステップで \(x\) に起きた変化」である。つまりこの TickTack システムの例では、\(t=0\) は次のステップで \(t=1\) となることから \(t'=1\) であり、同様に \(t=1\) は次のステップで \(t=1\) となることから \(t'=0\) である。これは: \[ \begin{eqnarray} {\it Next} & \ldef & {\sf IF} \ t=0 \ {\sf THEN} \ t'=1 \ {\sf ELSE \ IF} \ t=1 \ {\sf THEN} \ t'=0 \nonumber \\ & \equiv & (t = 0 \land t' = 1) \lor (t = 1 \land t' = 0) \label{next} \end{eqnarray} \] と表すことができる。

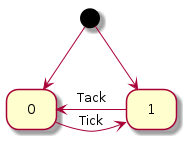
さて、ここまで定義できればこの TickTack システムを UML の状態遷移図で表すことも容易であろう。なお、この TickTack システムは宇宙における時間という概念が有効な限り停止することはない。

Fig 1. TickTack システムの状態遷移図。

基本的な TLA+ の記述

式 (\(\ref{init}\)) と (\(\ref{next}\)) より TickTack の仕様として必要なアサーションは以下のように表現できる。\[ \begin{eqnarray*} {\it Init} & \ldef & t \in \{0, 1\} \\ {\it Next} & \ldef & (t = 0 \land t' = 1) \lor (t = 1 \land t' = 0) \end{eqnarray*} \] TLA+ では \(t\) がどのような過程を経て \(t'\) に変化するかを詳細に説明することなく、ステップの前後の状態にのみ着目している。実際のプログラムで if 文を使うかビット反転命令を使うかは実装依存である。

この仕様を TLA+ で表現すると以下のような記述となる。順番に説明しよう。

---- MODULE TickTack ----
VARIABLES t
Init == t \in {0, 1}
tick == t = 0 /\ t' = 1
tack == t = 1 /\ t' = 0
Next == tick \/ tack
====
INIT Init
NEXT Next
Fig 2. TickTack システムの TLA+ 仕様記述。右はモデルファイ TickTack.cfg の内容。

TLA+ にはモジュールという大きな単位があり、1 行目と 7 行目のように ---- MODULE モジュール名 ---- で始まり ==== で終了する。またモジュール中の ---- は可読性のための罫線として使用することができる。これらは 4 文字以上連続する - または = であれば良い。

2 行目の VARIABLES は変数宣言でシステムで使用する状態変数を定義している (最後の S は省略可能で VARIABLE でも良い)。ここでは 0 または 1 のシステム状態を保持するために一つの変数 \(t\) を宣言している。

3 行目の Init はシステムの取りうる初期状態 \(t \in \{0,1\}\) を定義している。一般的なプログラミング言語が具体値を「代入」するのに対して、仕様記述言語では仕様が満たすべき条件を「定義」する点で少し意味が異なることに注意。

4-6 行目はシステムが次に取りうる状態を表す Next と、その部品となる tick および tack を定義している。TLA+ では /\ が論理積 \(\land\)、\/ が論理和 \(\lor\) を表している。

t' は次のステップで \(t\) がとるべき値である。したがって、例えば tick は \(t=0 \land t'=1\) つまり「ステップ開始時の \(t\) が 0 で次のステップに引き継ぐ \(t\) が 1 となる」というアサーションを定義している。これは条件文として if \(t=0\) then \(t'=1\) と等価とも言える。

システムの "取りうる初期状態" と "次に取りうる状態" の定義がモデルファイル TickTack.cfg の INIT と NEXT で指定できる。したがって Init と Next には任意の定義名をつけることができる。

またこの例では使用していないが TLA+ の記述では (* block comment *) と \* line comment 形式のコメントを使用することができる。

TLC 検証結果

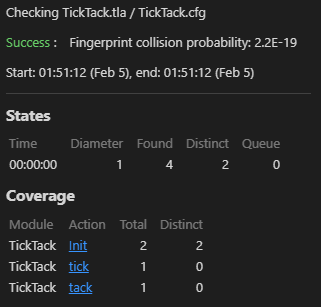
Fig 2 に示す仕様記述を検証すると (実行方法は TLC 検証参照) Fig 3 のような結果となり状態モデルに矛盾がないこと、つまり式 (\(\ref{init}\)) と (\(\ref{next}\)) に示す 2 つのアサーションが TickTack システムで取りうる全ての状態に対して成功することを確認することができる。

Fig 3. Fig 2 の検証結果。vscode での TLC の実行は TLC 検証を参照。

以上、TLA+ により TickTack システムの仕様は以下の 2 点に明文化されるステートマシンとして表現できることが確認できた。

  1. システムの初期状態は \(t \in \{0, 1\}\) である。
  2. 全てのステップで状態は \((t=0 \land t'=1) \lor (t=1 \land t'=0)\) である。

ここでカンのいい人は仕様に停止条件がないのになぜ TLC 検証が停止したかが気になったかもしれない。その話題については TLC 検査の特徴を参照。

エラーの検出

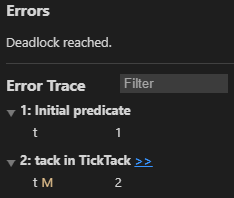
ではここで未定義の状態を生成するように修正を加えて TLC がどのように振る舞うかを見てみよう。Fig 4 は \(t=1\) の時に \(t'=2\) となる可能性を追加した仕様とその検証結果である。

Fig 4. 未定義の状態が発生するケースを追加したバージョンとその TLC チェック結果。

このエラートレースは「初期状態 \(t=1\) で開始し tack を通過したあとに \(t=2\) (未定義の状態) となり halt した」ということを伝えている。つまり設計者は \(t=2\) という予期しない状態を設計として排除するか、\(t=2\) となるケースを正しい仕様として考慮しなければならない。