構造的アルゴリズム

木構造

Takami Torao #BTree
  • このエントリーをはてなブックマークに追加

概要

木構造 (tree structure) はデータを階層的に表現するためのデータ構造である。ノード (頂点) とエッジ (辺) で構成されるグラフ構造の一種だが、閉路を持たない DAG である。

Table of Contents

  1. 概要
  2. AVL 木
  3. van Emde Boas 木
  4. 参照

AVL 木

van Emde Boas 木

van Emde Boas 木 (vEB; ファン・エムデ・ボアス木) [1] は大規模な整数集合に対して高速な存在判定、範囲検索、前後検索などを行うことのできるデータ構造である。キー範囲が事前に決まっている全体集合 (universe) での優先度付きキューや集合操作を効率的に実行する。整数の全体集合 \(\{0,1,\ldots,n-1\}\) に対して、挿入、削除、検索、先行値 (一つ先の要素)、後続値 (一つ後の要素)、最小値、最大値の取得といった操作を \(O(\log\log n)\) 時間で実行できる。これは従来の平衡二分木やヒープの \(O(\log n)\) 時間を大幅に改善した。

この構造は全体集合を \(\sqrt{n}\) 個のクラスタに分割し、各クラスタは再帰的に同じように分割されたツリー構造を持つ。具体的にはサイズ \(n\) の全体集合 \(U\) に対して、値となる整数を上位と下位のちょうど半分に分割し (つまり上位 \(\sqrt{n}\) ビットと下位 \(\sqrt{n}\) ビットに分割し)、上位を下層クラスタのインデックス、下位を下層を再帰的に検索するパラメータとして使用する。

Figure 1 は \(n=256\) (8 ビット) の van Emde Boas 木に値 162 を挿入する例である。まず、162 = 0b10100010 は上位 4 ビット 10 = 0b1010 と下位 4 ビット 2 = 0b0010 に分割され、第一階層 \({\rm vEB}_{256}\) のクラスタ 10 へ値 2 で進む。第2階層 \({\rm vEB}_{16}\) では値 2 = 0b0010 を上位 2 ビット 0 = 0b00 と下位 2 ビット 2 = 0b10 に分割し、クラスタ 0 へ値 2 で進む。この操作を葉まで繰り返し、最終的に存在を表す true を設定する。

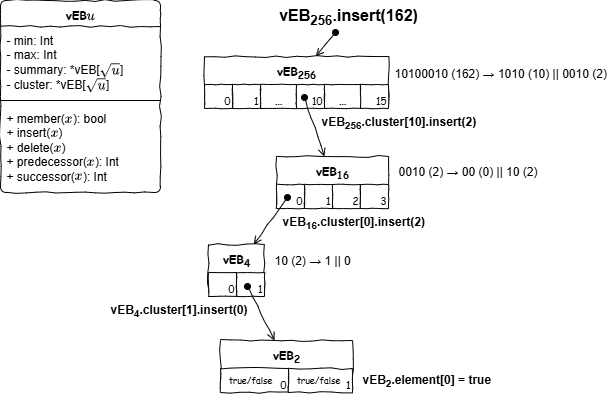
Figure 1. van Emde Boas 木での挿入操作。末端をブール値ではなく値を格納できるようにすれば Key-Value 型に拡張できる。

各ノードが、そのノードの配下に含まれる値の最小値と最大値を記録しているため、ある値の一つ前の値 (predecessor) と一つ後の値 (successor) も効率よく検索することができる。

Figure 2.

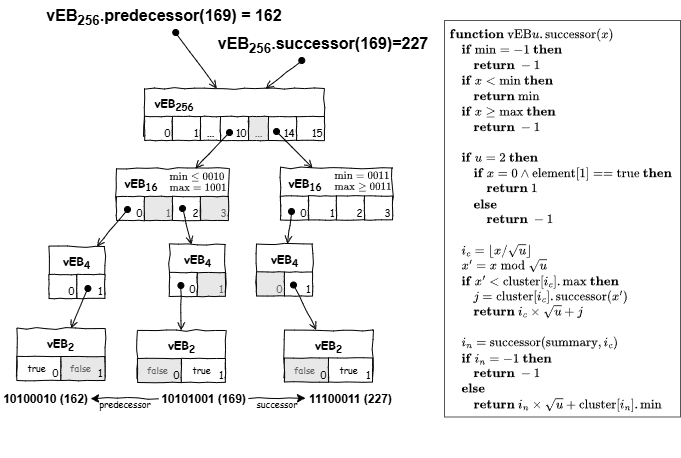
参照

  1. VAN EMDE BOAS, Peter. Preserving order in a forest in less than logarithmic time. In: 16th Annual Symposium on Foundations of Computer Science (sfcs 1975). IEEE, 1975. p. 75-84.

B-Tree

B-Tree または B 木は自己平衡型の多分木データ構造である。各ノードがソート済みの複数のキーと子ノードへの参照を持つことで、二分木より高さの低いツリー構造を形成することができる。このため検索や挿入、削除操作の効率が良く、特にディスクや SSD のようなストレージドライブに対する I/O を最適化するように設計できることから、大量のデータを効率的に管理するようなデータベースやファイルシステムなどで広く使用されている。…

2024年12月5日(Thu) #BTree

B+Tree

B-Tree の派生型である B+Tree は、個々のキーの検索効率を下げる代わりに、ある範囲のデータをまとめて取得するケース (レンジクエリー) に適した構造を持つ。B-Tree が中間ノードにもデータエントリを保持していたのに対して、B+Tree では末端の葉にのみエントリを保持し、葉は相互にリンクしたリストの構造を持っている。…

2018年4月15日(Sun) #BTree

論文翻訳: Lower Bounds for External Memory Dictionaries

検索操作においては従来の B-Tree の定数オーダーの性能を維持しながら、更新操作のスループットを大幅に改善する Bε-Tree についての 2003 年の論文。

2024年11月6日(Wed) 2003年の論文 #BTree #BεTree

論文翻訳: An Introduction to Bε-trees and Write-Optimization

B-Tree と似た構造を持ち、更新と挿入で高い性能を持つ Bε-Tree に関する 2015 年の記事。

2024年11月9日(Sat) 2015年の記事 #BTree #BεTree

論文翻訳: PRESERVING ORDER IN A FOREST IN LESS THAN LOGARITHMIC TIME

現在は van Emde Boas Tree として知られている、整数の優先度付きキューにおいて従来の \(O(\log n)\) 時間を破る \(O(\log\log n)\) 時間での操作を可能にする階層化二分木 (stratified binary tree) データ構造を提案する 1975 年の論文。…

2025年7月29日(Tue) 1975年の論文 #vanEmdeBoasTree #vEBTree