二項分布の推定

概要

事象 \(b \in \{0,1\}\) のベルヌーイ試行で \(b=1\) となる確率を \(p\)、試行回数を \(n\) とした時、1 が \(x\) 回観測される (出た数の合計が \(x\) となる) 確率関数は二項分布 \(P(x;n,p)\) に従う。ここで \(x=k\) となる確率は以下のように表される。\[ P(x=k|n,p) = \binom nk p^k (1-p)^{n-k} \]

二項分布の性質が \(K=2\) とした多項分布と等しいことからその推定も多項分布の推定で一般化される。

尤度関数 = 二項分布の同時確率

この確率分布にもとづく確率変数 \(x\) が \(m\) 個の標本の組み合わせ \((x_1, x_2, \ldots, x_m) = \vector{x}\), \(0 \leq x_i \leq n\) として観測されたとする。このときの同時確率は以下のように表される。\[ \begin{eqnarray} P(\vector{x}|n,p) & = & \prod_{i=1}^m \binom n{x_i} p^{x_i} (1-p)^{n-{x_i}} \nonumber \\ & = & {}_n\mathrm{C}_{x_1} {}_n\mathrm{C}_{x_2} \cdots {}_n\mathrm{C}_{x_m} p^{\sum_{i=1}^m x_i} (1-p)^{mn-\sum_{i=1}^m x_i} \label{likelihood_function} \end{eqnarray} \]

実際にデータ \((x_1, x_2, \ldots, x_m) = \vector{x}\) を観測したとき \(P(x_1,\cdots,x_m|n,p)\) は \(\vector{x}\) に対する推定値 \(\mu\) の確度を表す尤度関数となる。ここで対数尤度関数は以下のように表される。\[ \begin{equation} \label{log_likelihood} \log P(\vector{x}|n,p) = \log \left( \prod_{i=1}^m {}_n\mathrm{C}_{x_i} \right) + \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) \end{equation} \]

最尤推定

最尤推定は (対数) 尤度関数が最大値を取る \(\hat{\mu}_{\rm mle}\) を求める。\(\hat{\mu}_{\rm mle}\) は対数尤度関数 (\(\ref{log_likelihood}\)) が極値となる位置の \(p\) である。したがって対数尤度関数の微分値が 0 となる位置の \(p\) を求める。\[ \frac{\partial}{\partial p} \left\{ \log \left( \prod_{i=1}^m {}_m\mathrm{C}_{x_i} \right) + \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) \right\} \\ = \frac{1}{p} \sum_{i=1}^m x_i - \frac{1}{1-p} \left(mn - \sum_{i=1}^m x_i\right) = 0 \] したがって \[ \hat{\mu}_{\rm mle} = \frac{1}{mn}\sum_{i=1}^m x_i = \frac{1}{n} \bar{x} \] ここで \(\bar{x} = \frac{1}{m}\sum_{i=1}^m x_i\) は観測値 \(\vector{x}\) の相加平均である。

MAP推定

MAP 推定はベイズ定理における事後確率 \(P(\mu|\vector{x})\) を最大化する \(\hat{\mu}_{\rm map}\) を求める。\[ P(p|\vector{x}) = \frac{P(\vector{x}|p) P(p)}{P(\vector{x})} \]

エビデンスの \(P(\vector{x})\) はすでに観測済みの \(\vector{x}\) に対する確率であり、事後確率が最大となる \(p\) の結果には関与しないため無視する。\[ P(p|\vector{x}) \propto P(\vector{x}|p) P(p) = P(x_1|p) P(x_2|p) \cdots P(x_m|p) P(p) \]

ここで尤度関数 \(P(\vector{x}|p)\) は (\(\ref{likelihood_function}\)) で表されている。事前確率 \(P(p)\) はベータ分布と正規分布の 2通りで考えてみよう。

事前確率 = ベータ分布

ベータ分布は二項分布の自然共役分布であることから二項分布の事前確率を表すのによく用いられている。\[ \begin{eqnarray} {\rm Beta}(x;\alpha,\beta) & = & \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}, \,\,\, B(\alpha,\beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \label{betadistribution} \\ \log {\rm Beta}(x;\alpha,\beta) & = & \log \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \nonumber \\ & = & (\alpha-1) \log x + (\beta-1) \log (1-x) + \log \frac{1}{B(\alpha,\beta)} \label{logbetadistribution} \end{eqnarray} \] \(B(\alpha,\beta)\) はベータ関数だが \(x\) には関与していないため後の \({\rm argmax}\) 操作や微分で取り除くことができる。

分布の対数をとっても事後確率が最大化する位置の \(\mu\) には影響しないことから計算の単純化のため対数化する。\[ \begin{align*} \hat{\mu}_{{\rm map}} & = \argmax_{p} P(p|\vector{x}) = \argmax_{p} \log P(p|\vector{x}) = \argmax_{p} \log P(\vector{x}|p) P(p) \\ & = \argmax_{p} \left[ \left\{ \log \left( \prod_{i=1}^m {}_m\mathrm{C}_{x_i} \right) + \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) \right\} + \left\{ (\alpha-1) \log p + (\beta-1) \log (1-p) + \log \frac{1}{B(\alpha,\beta)} \right\} \right] \\ & = \argmax_{p} \left\{ \left(\alpha-1+\sum_{i=1}^m x_i \right) \log p + \left(\beta - 1 + mn - \sum_{i=1}^m x_i\right) \log (1-p) \right\} \end{align*} \]

\(p\) で偏微分して 0 となる極値を求めると MAP 推定の観点で最も確度の高い \(\hat{\mu}_{\rm map}\) が得られる。\[ \frac{\partial}{\partial p} \left\{ \left(\alpha-1+\sum_{i=1}^m x_i \right) \log p + \left(\beta - 1 + mn - \sum_{i=1}^m x_i\right) \log (1-p) \right\} \\ = \frac{1}{p}\left(\alpha-1+\sum_{i=1}^m x_i\right) - \frac{1}{1-p}\left(\beta-1+mn-\sum_{i=1}^m x_i\right) = 0 \\ (1-p) \left(\alpha-1+\sum_{i=1}^m x_i\right) - p \left(\beta-1+mn-\sum_{i=1}^m x_i\right) = 0 \] \[ \begin{align*} \left(\alpha-1+\sum_{i=1}^m x_i\right) & = p \left\{ \left(\alpha-1+\sum_{i=1}^m x_i\right) + \left(\beta-1+mn-\sum_{i=1}^m x_i\right) \right\} \\ & = \left(\alpha + \beta + mn - 2\right) p \end{align*} \]

少々煩雑になったが最終的に \(\hat{\mu}_{\rm map}\) は以下の式にまとめることができる。\[ \begin{equation} \label{map_mu} \hat{\mu}_{\rm map} = \frac{\alpha - 1 + \sum_{i=1}^m x_i}{\alpha + \beta + mn - 2} \end{equation} \]

ここで \(\alpha = \beta = 1\) と置くと \(\hat{\mu}_{\rm map} = \frac{\sum x}{mn}\) となり最尤推定での \(\hat{\mu}_{\rm mle}\) と等しくなることが分かる。これはベータ分布 \(P(p)={\rm Beta}(x; \alpha=1,\beta=1)={\rm Const.}\) より事後確率分布が尤度と同じ分布になるためである。

事前確率 = 正規分布

正規分布 (normal distribution) は平均 \(\mu\) と分散 \(\sigma^2\) をパラメータとした以下の式で表される。\[ \begin{align*} P(x| \mu,\sigma^2) & = \frac{1}{\sqrt{2\pi\sigma^2}} {\rm exp}\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\} \\ \log P(x|\mu,\sigma^2) & = \log \frac{1}{\sqrt{2\pi\sigma^2}} - \frac{(x-\mu)^2}{2\sigma^2} \end{align*} \]

事前確率 \(P(p)\) はベイズ更新を行う上で尤度 \(P(x|p)\) の共役分布を選択すると便利というものであって、尤度のブレとして想定できる分布であれば主観で決めて良い。正規分布を適用するとどうなるか試してみる。

ベータ分布と同様に、分布の対数をとっても事後確率が最大化する位置の \(\hat{\mu}_{\rm map}\) には影響しないことから計算の単純化のため対数化する。\[ \begin{align*} \hat{\mu}_{{\rm map}} & = \argmax_{p} P(p|\vector{x}) = \argmax_{p} \log P(p|\vector{x}) = \argmax_{p} \log P(\vector{x}|p) P(p) \\ & = \argmax_{p} \left[ \left\{ \log \left( \prod_{i=1}^m {}_m\mathrm{C}_{x_i} \right) + \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) \right\} + \left\{ \log \frac{1}{\sqrt{2\pi\sigma^2}} -\frac{(p-\mu)^2}{2\sigma^2} \right\} \right] \\ & = \argmax_{p} \left\{ \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) - \frac{(p-\mu)^2}{2\sigma^2} \right\} \end{align*} \]

\(p\) で偏微分して 0 となる極値を求めると三次方程式が現れる。\[ \frac{\partial}{\partial p} \left\{ \sum_{i=1}^m x_i \log p + \left(mn - \sum_{i=1}^m x_i\right) \log (1-p) - \frac{(p-\mu)^2}{2\sigma^2} \right\} \\ = \frac{1}{p} \sum_{i=1}^m x_i - \frac{1}{1-p}\left(mn-\sum_{i=1}^m x_i\right) - \frac{p-\mu}{\sigma^2} = 0 \\ (1-p) \sum_{i=1}^m x_i - p \left(mn-\sum_{i=1}^m x_i\right) - p (1-p) \frac{p-\mu}{\sigma^2} = 0 \\ p^3 - (\mu + 1) p^2 + (1 - mn \sigma^2) p - \sigma^2 \sum_{i=1}^m x_i = 0 \] 結果は Wolfram|Alpha を参照。ベータ分布と異なりこの解はかなり複雑な形をしている。事前分布は主観で選択しても良いとはいえ尤度関数との相性で \(p\) を求める難易度が大きく違ってくる。

ベイズ推定

最尤推定、MAP 推定がもっとも確率の高くなる位置の \(p\) を導出していたのに対して (点推定) ベイズ推定は確率分布を導出する (区間推定)。

ベイズの定理より、尤度関数とする二項分布 (\(\ref{likelihood_function}\)) に事前確率とするベータ分布 (\(\ref{betadistribution}\)) を掛けると、事後分布 \(P(p|\vector{x})\) はベータ分布 \({\rm Bin}(p;\alpha,\beta)\) に比例していることが分かる (言い換えると事後確率はベータ分布の形をしている)。\[ \begin{align*} P(p|\vector{x}) & \propto {\rm Bin}(\vector{x}|p) \, {\rm Beta}(p; \alpha,\beta) \\ & \propto p^{\sum_{i=1}^m x_i} (1-p)^{mn - \sum_{i=1}^m x_i} p^{\alpha-1} (1-p)^{\beta-1} \\ & = p^{(\alpha+\sum_{i=1}^m x_i)-1} (1-p)^{(\beta+mn-\sum_{i=1}^m x_i)-1} \end{align*} \]

ベータ分布は積分して 1 となる確率密度関数であるため、上式に正規化項 \(\frac{1}{B(\alpha,\beta)}\) を掛ければ事後確率となる。\[ \begin{eqnarray} P(p|\vector{x}) & = & \frac{p^{(\alpha+\sum_{i=1}^m x_i)-1} (1-p)^{(\beta+mn-\sum_{i=1}^m x_i)-1}}{B(\alpha,\beta)} \nonumber \\ & = & {\rm Beta}(p;\alpha+\sum_{i=1}^m x_i, \beta+mn-\sum_{i=1}^m x_i) \label{posterior} \end{eqnarray} \]

式の意味は非常に簡単である。\(p\) を 1 の出る確率とする \(b \in \{0,1\}\) のベルヌーイ試行を \(n\times m\) 回行ったと見ると、\(\alpha\) に 1 の出た回数を、\(\beta\) に 0 の出た回数を加算していると見ることができる。それぞれ \(N_1, N_0\) とすると: \[ {\rm Beta}(p;\alpha+N_1, \beta+N_0) \]

事後確率 (\(\ref{posterior}\)) の期待値、分散はベータ分布のそれらと同じである。MAP 推定で導いた \(\hat{\mu}_{\rm MAP}\) は事後確率のピークを求めているためベータ分布の最頻値と等しい。

多項分布のベイズ推定で求めた事後確率は以下の置き換えで二項分布の事後確率に変形することができる。\[ {\rm Dir}(\vector{p}; \vector{\alpha} + \vector{x}) \left\{ \begin{array}{l} K \to 2 \\ \vector{\alpha} \to (\beta, \alpha) \\ \vector{x} \to (N_0, N_1) \\ \vector{p} \to (1-p, p) \end{array} \right\} {\rm Beta}(p; \alpha + N_1, \beta+N_0) \]

実用例

例1: 未知のじゃんけん

二項分布において勝敗や成功/失敗、正常/異常のような \(x_i \in \{0, 1\}\)、\(n=1\) の事象はベルヌーイ分布と等価である。

勝率が未知のじゃんけんで5回すべて勝ったとき試行回数 \(m = 5\) のうち5回勝利していることから \(\vector{x} = (1, 1, 1, 1, 1)\) と見なすことができる。

最尤推定での勝率は \[ \hat{\mu}_{\rm mle} = \frac{5}{5} = 1.00 \] となり勝率 100% と言う結果になる。\(\alpha = \beta\) とした MAP 推定に基づいた勝率は \[ \hat{\mu}_{\rm map} = \frac{\alpha - 1 + 5}{\alpha + \alpha + 5\times 1 - 2} = \frac{\alpha + 4}{2\alpha + 3} \]

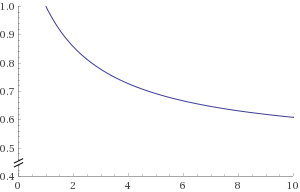
ここで \(\alpha\) に対する \(\hat{\mu}_{\rm map}\) は右のグラフのように推移する。

\(\alpha=1\) の時に \(\hat{\mu}_{\rm map}=1\)、つまり勝率 100% で最尤推定での結果と一致する。

\(\alpha\) が大きくなるにつれ観測値 \(x\) が推定に及ぼす影響が少なくなり、事前の想定がない状態での平均 \(\frac{1}{n}\) に近づいてゆく。

例2: 1～5 点で評価する商品口コミサイトの推定評価

評価 1～5 の取り得る事象を\(x = {\sf 評価}-1\) と置き換えると \(x_i \in \{0, 1, 2, 3, 4\}\) より \(n=4\) である。

ある商品 A が 4 人の評価により 4, 3, 4, 5 点を得ている場合、二項分布に従う \(m = 4\) 回の試行で \(\vector{x} = (3, 2, 3, 4)\) という結果を得たと考えられる。このとき、最尤推定と MAP 推定 (\(\alpha = \beta = 2\)) を使ってもっとも確度の高い \(p = \hat{\mu}\) を求め、商品 A の推定評価を逆算すると: \[ \begin{align*} 4\times \hat{\mu}_{\rm mle} + 1 & = 4\times\frac{12}{4\times 4}+1 & = 4.00 \\ 4\times \hat{\mu}_{\rm map} + 1 & = 4\times\frac{2 - 1 + 12}{2 + 2 + 4\times 4 - 2}+1 & = 3.89 \end{align*} \] となる。

別の商品 B は大衆向けではないがマニアな 1 名によって最高得点の 5 を付けられた。つまり \(m=1, \vector{x}=(4)\) より商品 B の推定評価を求めると: \[ \begin{align*} 4\times \hat{\mu}_{\rm mle} + 1 & = 4\times\frac{4}{1\times 4}+1 & = 5.00 \\ 4\times \hat{\mu}_{\rm map} + 1 & = 4\times\frac{2 - 1 + 4}{2 + 2 + 1\times 4 - 2} & = 4.333 \end{align*} \]

このように MAP 推定は最尤推定に比べてサンプルが少ない状況で過度に結果にフィッティングしてしまう過学習を抑えることができる。